➤ How to Code a Game
➤ Array Programs in Java
➤ Java Inline Thread Creation
➤ Java Custom Exception
➤ Hibernate vs JDBC
➤ Object Relational Mapping
➤ Check Oracle DB Size
➤ Check Oracle DB Version
➤ Generation of Computers
➤ XML Pros & Cons
➤ Git Analytics & Its Uses
➤ Top Skills for Cloud Professional
➤ How to Hire Best Candidates
➤ Scrum Master Roles & Work
➤ CyberSecurity in Python
➤ Protect from Cyber-Attack
➤ Solve App Development Challenges
➤ Top Chrome Extensions for Twitch Users
➤ Mistakes That Can Ruin Your Test Metric Program
What is Strassen’s matrix multiplication algorithm? What is the different algorithm for matrix multiplication? What is Divide and Conquer Matrix Multiplication? The different time complexity for different matrix multiplication algorithm? Here we will discuss all of them.
There are three methods to find Matrix Multiplication. These are,
1) Naive Method
2) Divide and Conquer Method
3) Strassen’s Method
Table Of Contents
- Naive Method of Matrix Multiplication
- Divide and Conquer Method
- Strassen’s Matrix Multiplication Algorithm
Naive Method of Matrix Multiplication
It is the traditional method which we use in general. It can be defined as,
Let A be an m × k matrix and B be a k × n matrix. The product of A and B, denoted by AB, is m × n matrix with its (i, j )th entry equal to the sum of the products of the corresponding elements from the ith row of A and the jth column of B. In other words, if AB =[cij], then cij = ai1b1j + ai2b2j +···+aikbkj.
Condition for the Matrix multiplication:- The product of two matrices is not defined when the number of columns in the first matrix and the number of rows in the second matrix are not the same.
Example of Matrix Multiplication,
Matrix A =
a11 a12
a21 a22
Matrix B =
b11 b12
b21 b22
The product of A and B is denoted as AB and it can be calculated as AB=(a11*b11+a12*b21) (a11*b12+a12*b22)
(a21*b11+a22*b21) (a21*b12+a22*b22)
Example using 2×2 matrices,
1 3
A =
7 5
6 8
B =
4 2
1*6+3*4 1*8+3*2
C =
7*6+5*4 7*8+5*2
18 14
C =
62 66Algorithm for Naive Method of Matrix Multiplication
square_matrix_multiply(a, b)
n = a.rows
let c be a new n x n matrix
for i = 1 to n
for j = 1 to n
cij = 0
for k=1 to n
cij = cij + (aik * bkj)
return cWhy it needs three for loops? For accessing all the elements of any matrix we need two for loops. But for finding the product, it requires one additional for loop. That’s how it is taking 3 for loops.
Time complexity:- O(n3)
Java Method to find Matrix Multiplication for Square Matrix using the above method,
// method to calculate product of two matrix
public static int[][] multiplyMatrix(int[][] a, int[][] b) {
// find size of matrix
// (Assuming both matrix is square matrix
// of same size)
int size = a.length;
// declare new matrix to store result
int product[][] = new int[size][size];
// find product of both matrices
// outer loop
for (int i = 0; i < size; i++) {
// inner-1 loop
for (int j = 0; j < size; j++) {
// assign 0 to the current element
product[i][j] = 0;
// inner-2 loop
for (int k = 0; k < size; k++) {
product[i][j] += a[i][k] * b[k][j];
}
}
}
return product;
}Divide and Conquer Method
What is divide and conquer method? In the divide and conquer method we say that if the problem is larger then we break the problem into sub-problems and solve those sub-problems. Later combine the solutions of sub-problems to get the solution for the actual problem.
If it is a smaller problem then it can be solved directly but if it is a large problem then using divide and conquer break them into small problems. Therefore let us see the solution for the smaller problems.
To solve our problem assume 2×2 is the smallest square matrix. Let A and B are two different matrices.
a11 a12
A =
a21 a22 b11 b12
B =
b21 b22 c11 c12
C =
c21 c22Where C = A*B, The Matrix C can be calculated as,
- c11 = a11*b11 + a12*b21
- c12 = a11*b12 + a12*b22
- c21 = a21*b11 + a22*b21
- c22 = a21*b12 + a22*b22
Since this method requires 8 multiplication and 4 addition, therefore, it requires constant time.
What if the size is greater than 2×2? We assume that the matrices are having dimensions in powers of 2 like 2×2, 4×4, 8×8, 16×16, 256×256, and e.t.c. If it is not of power 2×2 then we can fill zeros and makes it a square matrix of power of 2×2.
Example Using 4×4
Since it is a larger problem therefore we must divide it into smaller problems and then solve those sub-problem and combine the solutions.
Following is the simple divide and conquer method to multiply two 4×4 square matrices,
a) Divide both matrices in 4 sub-matrices of size 2×2 (i.e. n/2 x n/2 where n=4)
b) Then calculate the values recursively.
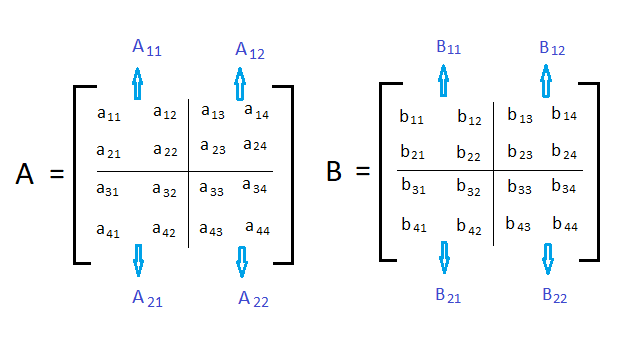
Algorithm of Divide and Conquer for Matrix Multiplication
MatrixMultiply(a, b)
n = a.rows
let c be a new n x n matrix
if n == 1
c11 = a11 * b11
else partition a, b, and c
C11 = MatrixMultiply(A11, B11) + MatrixMultiply(A12, B21)
C12 = MatrixMultiply(A11, B12) + MatrixMultiply(A12, B22)
C21 = MatrixMultiply(A21, B11) + MatrixMultiply(A22, B21)
C22 = MatrixMultiply(A21, B12) + MatrixMultiply(A22, B22)
return cIt has 8 recursive function calls which call itself, and it contains 4 addition. These additions are matrices addition, not the normal addition. The time complexity for the addition of two matrices is O(N2).
Recurance relation T(N),
=> 8T(N/2) + O(N2) if n>1
=> O(1) if n=1
Time complexity = O(N3)
Whether we are using the naive method or the divide-conquer method to find matrix multiplication its time complexity is O(N3).
Cons of Divide and Conquer over Naive Method:- Since the divide and conquer method uses the recursion technique, therefore, it internally uses the stack and consumes extra spaces. In terms of space complexity, the basic naive method is better than the divide and conquer technique of matrix multiplication.
Strassen’s Matrix Multiplication Algorithm
The major work in matrix multiplication is multiplication only. So, the idea is:- If we reduced the number of multiplications then that will make the matrix multiplication faster.
Strassen had given another algorithm for finding the matrix multiplication. Unlike a simple divide and conquer method which uses 8 multiplications and 4 additions, Strassen’s algorithm uses 7 multiplications which reduces the time complexity of the matrix multiplication algorithm a little bit.
The addition and Subtraction operation takes less time compared to the multiplication process. In Strassen’s matrix multiplication algorithm, the number of multiplication was reduced but the number of addition and subtraction increased.
Strassen’s Matrix Multiplication Algorithm
From the previous diagram,
P1 = (A11 + A22) * (B11 + B22)
P2 = (A21 + A22) * B11
P3 = A11 * (B12 – B22)
P4 = A22 * (B21 – B11)
P5 = (A11 + A12) * B22
P6 = (A21 – A11) * (B11 + B12)
P7 = (A12 – A22) * (B21 + B22)
C11 = P1 + P4 – P5 + P7
C12 = P3 + P5
C21 = P2 + P4
C22 = P1 – P2 + P3 + P6
Recurance Relation T(N),
=> 7T(N/2) + O(N2) if n>1
=> O(1) if n=1
Time complexity = O(n log 7/2) = O(n2.8074)
The O(n2.8074) is slightly lesser than O(n3) but this method is usually not preferred for practical purposes.
The constants used in Strassen’s method are high and most of the time the Naive method works better. To find multiplication of Sparse matrices (which contains very few non-zero elements) better algorithms are available. The submatrices in recursion take extra space. Because of the limited precision of computer arithmetic on non-integer values, larger errors accumulate in Strassen’s algorithm than in the Naive Method.
Java Program to Implement Strassen’s Matrix Multiplication Algorithm
Java program to Implement Strassen’s Matrix Multiplication Algorithm using methods and by taking input values from the user,
/**
** Java Program to Implement Strassen Algorithm
**/
package com.know.program;
import java.util.Scanner;
public class Matrix {
// create Scanner class object to read input
private static Scanner scan = new Scanner(System.in);
// method to calculate product of two matrix
// Strassen Algorithm
public int[][] multiply(int[][] a, int[][] b) {
// find size of matrix
int n = a.length;
// create new matrix to store resultant
int[][] c = new int[n][n];
/** base case **/
if (n == 1)
c[0][0] = a[0][0] * b[0][0];
else { /* general case */
int[][] A11 = new int[n / 2][n / 2];
int[][] A12 = new int[n / 2][n / 2];
int[][] A21 = new int[n / 2][n / 2];
int[][] A22 = new int[n / 2][n / 2];
int[][] B11 = new int[n / 2][n / 2];
int[][] B12 = new int[n / 2][n / 2];
int[][] B21 = new int[n / 2][n / 2];
int[][] B22 = new int[n / 2][n / 2];
// divide matrix A into 4 halves
split(a, A11, 0, 0);
split(a, A12, 0, n / 2);
split(a, A21, n / 2, 0);
split(a, A22, n / 2, n / 2);
// divide matrix B into 4 halves
split(b, B11, 0, 0);
split(b, B12, 0, n / 2);
split(b, B21, n / 2, 0);
split(b, B22, n / 2, n / 2);
/**
* p1 = (A11 + A22)(B11 + B22)
* p2 = (A21 + A22) B11
* p3 = A11 (B12 - B22)
* p4 = A22 (B21 - B11)
* p5 = (A11 + A12) B22
* p6 = (A21 - A11) (B11 + B12)
* p7 = (A12 - A22) (B21 + B22)
**/
int[][] p1 = multiply(add(A11, A22), add(B11, B22));
int[][] p2 = multiply(add(A21, A22), B11);
int[][] p3 = multiply(A11, sub(B12, B22));
int[][] p4 = multiply(A22, sub(B21, B11));
int[][] p5 = multiply(add(A11, A12), B22);
int[][] p6 = multiply(sub(A21, A11), add(B11, B12));
int[][] p7 = multiply(sub(A12, A22), add(B21, B22));
/**
* C11 = p1 + p4 - p5 + p7
* C12 = p3 + p5
* C21 = p2 + p4
* C22 = p1 - p2 + p3 + p6
**/
int[][] C11 = add(sub(add(p1, p4), p5), p7);
int[][] C12 = add(p3, p5);
int[][] C21 = add(p2, p4);
int[][] C22 = add(sub(add(p1, p3), p2), p6);
// join 4 halves into one result matrix
join(C11, c, 0, 0);
join(C12, c, 0, n / 2);
join(C21, c, n / 2, 0);
join(C22, c, n / 2, n / 2);
} // end-of-else-part
// return resultant matrix
return c;
}
// method to add two matrices
public int[][] add(int[][] a, int[][] b) {
int n = a.length;
int[][] c = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
c[i][j] = a[i][j] + b[i][j];
return c;
}
// method to subract two matrices
public int[][] sub(int[][] a, int[][] b) {
int n = a.length;
int[][] c = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
c[i][j] = a[i][j] - b[i][j];
return c;
}
// method to split parent matrix into child matrices
public void split(int[][] parentMatrix, int[][] childMatrix,
int fromIndex, int toIndex) {
for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++)
for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++)
childMatrix[i1][j1] = parentMatrix[i2][j2];
}
// method to join child matrices into parent matrix
public void join(int[][] childMatrix, int[][] parentMatrix,
int fromIndex, int toIndex) {
for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++)
for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++)
parentMatrix[i2][j2] = childMatrix[i1][j1];
}
// method to read matrix elements as input
public int[][] readMatrix(int[][] temp) {
for (int i = 0; i < temp.length; i++) {
for (int j = 0; j < temp[0].length; j++) {
// read matrix elements
temp[i][j] = scan.nextInt();
}
}
return temp;
}
// main method
public static void main(String[] args) {
System.out.println("Strassen's Matrix "+
"Multiplication Algorithm Test\n");
// Create an object of Matrix class
Matrix mtx = new Matrix();
// declare variables
int size = 0;
int a[][] = null; // first matrix
int b[][] = null; // second matrix
int c[][] = null; // resultant matrix
System.out.print("Enter Matrix Order: ");
size = scan.nextInt();
// initialize matrices
a = new int[size][size];
b = new int[size][size];
c = new int[size][size];
// read matrix A and B
System.out.println("Enter Matrix A: ");
a = mtx.readMatrix(a);
System.out.println("Enter Matrix B: ");
b = mtx.readMatrix(b);
// multiplication of matrix
c = mtx.multiply(a, b);
// display resultant matrix
System.out.println("Resultant Matrix: ");
for(int i=0; i<c.length; i++) {
for(int j=0; j<c[0].length; j++) {
System.out.print(c[i][j]+" ");
}
System.out.println(); // new line
}
}
}Output for different test-cases:-
Strassen’s Matrix Multiplication Algorithm Test
Enter Matrix Order: 2
Enter Matrix A:
1 3
7 5
Enter Matrix B:
6 8
4 2
Resultant Matrix:
18 14
62 66
Strassen’s Matrix Multiplication Algorithm Test
Enter Matrix Order: 4
Enter Matrix A:
5 2 6 1
0 6 2 0
3 8 1 4
1 8 5 6
Enter Matrix B:
7 5 8 0
1 8 2 6
9 4 3 8
5 3 7 9
Resultant Matrix:
96 68 69 69
24 56 18 52
58 95 71 92
90 107 81 142
If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!