➤ How to Code a Game
➤ Array Programs in Java
➤ Java Inline Thread Creation
➤ Java Custom Exception
➤ Hibernate vs JDBC
➤ Object Relational Mapping
➤ Check Oracle DB Size
➤ Check Oracle DB Version
➤ Generation of Computers
➤ XML Pros & Cons
➤ Git Analytics & Its Uses
➤ Top Skills for Cloud Professional
➤ How to Hire Best Candidates
➤ Scrum Master Roles & Work
➤ CyberSecurity in Python
➤ Protect from Cyber-Attack
➤ Solve App Development Challenges
➤ Top Chrome Extensions for Twitch Users
➤ Mistakes That Can Ruin Your Test Metric Program
Arrays Data Structures and Algorithms | Let us examine some common and popular algorithms and problems related to array data structure. We will also discuss the following algorithms:- Kadane’s algorithm, and the Boyer-Moore Voting algorithm. We will also see prefix sum and two-pointer approaches.
The time complexity for different operations on an array:-
- Insert: O(n)
- Search: O(n) for an unsorted array. O(log n) for sorted array.
- Delete: O(n)
- Get ith element: O(1)
- Update ith element: O(1)
However, insert at the end and delete from the end can be done in O(1) time.
Table of Contents
- 1. Search Operations (Unsorted Array)
- 2. Largest Element in Array
- 3. Check If the Array is Sorted or Not
- 4. Find Second Largest Element
- 5. Find Unique Elements From Sorted Array
- 6. Move All Zeros to the End
- 7. Reverse an Array
- 8. Left Rotate An array by One
- 9. Left Rotate an array by D
- 10. Leaders in an array
- 11. Maximum Difference
- 12. Frequencies in a sorted Array
- 13. Stock Buy and Sell
- 14. Trapping Rain Water
- 15. Maximum Consecutive 1s
- 16. Maximum Length Even Odd Subarray
- 17. Kadane’s Algorithm
- 18. Majority Element in an Array
- 19. Minimum Group Filps to Make the same
- 20. Windows Sliding Techniques
- 21. Prefix sum
1. Search Operations (Unsorted Array)
I/P: arr = {20, 5, 7, 25}, x = 5; O/P: 1
Return -1 if not found.
public class Test {
public static void main(String[] args) {
int arr[] = { 20, 5, 7, 25 };
int x = 5;
System.out.println(search(arr, x));
}
// linear search
private static int search(int[] arr, int x) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == x) {
return i;
}
}
return -1;
}
}Time Complexity O(n) for the unsorted array.
2. Largest Element in Array
public class Test {
public static void main(String[] args) {
int arr[] = { 20, 5, 7, 25 };
System.out.println(largest(arr));
}
private static int largest(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (max < arr[i]) {
max = arr[i];
}
}
return max;
}
}Using Java 8 Stream:-
int largestElement = Arrays.stream(arr).max().getAsInt();
System.out.println(largestElement);Time Complexity O(n), and Auxiliary Space O(1).
3. Check If the Array is Sorted or Not
public class Test {
public static void main(String[] args) {
// int arr[] = { 20, 5, 7, 25 };
int arr[] = { 2, 5, 7, 25 };
boolean sorted = true;
for (int i = 1; i < arr.length; i++) {
if (arr[i - 1] > arr[i]) {
sorted = false;
break;
}
}
System.out.println(sorted);
}
}Time Complexity O(n), and Auxiliary Space O(1).
4. Find Second Largest Element
public class Test {
public static void main(String[] args) {
int arr[] = { 20, 5, 7, 20, 15 };
System.out.println(secondLargest(arr));
}
private static int secondLargest(int[] arr) {
int max = arr[0], secLg = Integer.MIN_VALUE;
for (int k : arr) {
if (max < k) {
secLg = max;
max = k;
} else if (k < max && k > secLg) {
secLg = k;
}
}
return secLg == Integer.MIN_VALUE ? -1 : secLg;
}
}Time Complexity O(n), and Auxiliary Space O(1). In the array 20 occurs 2 times, so both should be considered the largest number. Hence, 15 is the second largest number.
5. Find Unique Elements From Sorted Array
Find the unique elements from the array, and put them in the same array at the beginning. Use the same array to store the unique elements at the beginning of the array. While display ignore the remaining part of the array.
public class Test {
public static void main(String[] args) {
int arr[] = { 10, 20, 20, 30, 30, 30, 30 };
showUniqueElementsInSorted(arr);
}
private static void showUniqueElementsInSorted(int[] arr) {
int uniqueIndex = 1;
for (int i = 1; i < arr.length; i++) {
if (arr[i] != arr[i - 1]) {
arr[uniqueIndex] = arr[i];
uniqueIndex++;
}
}
// display 0 to uniqueIndex-1
for (int i = 0; i < uniqueIndex; i++) {
System.out.print(arr[i] + " ");
}
}
}Time Complexity O(n), and Auxiliary Space O(1).
6. Move All Zeros to the End
A given array can contain multiple zeros. Move all the zeros to the end of the array and preserve the order of other elements. Problem: 283. Similar Problem: 27
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int arr[] = { 8, 5, 0, 10, 0, 20 };
int nonZero = 0;
for (int i = 0; i < arr.length; i++) {
if (arr[i] != 0) {
swap(arr, i, nonZero);
nonZero++;
}
}
System.out.println(Arrays.toString(arr));
}
private static void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}Time Complexity O(n), and Auxiliary Space O(1).
To avoid swapping with itself, we can add the following check:-
for (int i = 0; i < n; i++) {
if (arr[i] != 0) {
// to avoid swapping with itself
if (i != nonZero) {
swap(arr, i, nonZero);
}
nonZero++;
}
}7. Reverse an Array
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int arr[] = { 8, 5, 0, 10, 0, 20 };
for (int i = 0, j = arr.length - 1; i < j; i++, j--) {
swap(arr, i, j);
}
System.out.println(Arrays.toString(arr));
}
private static void swap(int arr[], int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}Time Complexity O(n), and Auxiliary Space O(1).
8. Left Rotate An array by One
I/P: {1, 2, 3, 4, 5}
O/P: {2, 3, 4, 5, 1}
The counterclockwise rotation is called as left rotation.
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5 };
int temp = arr[0];
for (int i = 1; i < arr.length; i++) {
arr[i - 1] = arr[i];
}
arr[arr.length - 1] = temp;
System.out.println(Arrays.toString(arr));
}
}Time Complexity O(n), and Auxiliary Space O(1).
9. Left Rotate an array by D
The solution should be in place, i.e. without using another array. Assume D <= Number of elements in the array. If D is greater than n then modify it as:- d = d % n.
I/P: arr = {1, 2, 3, 4, 5}, k = 2
O/P: arr = {3, 4, 5, 1, 2}
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5 };
int d = 2;
leftRotate(arr, d);
System.out.println(Arrays.toString(arr));
}
private static void leftRotate(int[] arr, int d) {
reverse(arr, 0, d - 1);
reverse(arr, d, arr.length - 1);
reverse(arr, 0, arr.length - 1);
}
// both i & j are inclusive
private static void reverse(int[] arr, int i, int j) {
while (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
}Time complexity: θ(d + (n-d) + n) = θ(2n) = θ(n), Space complexity: θ(1)
Right Rotate By D
To right-rotate the array by k positions, you can follow a similar approach to the left rotation but with a slight modification in the steps. Instead of reversing the first k elements and then the remaining elements, you need to reverse the last k elements first, then the first n - k elements, and finally reverse the entire array. Here’s how you can do it:
private static void rightRotateByK(int[] arr, int d) {
int n = arr.length;
d = d % n; // In case d is larger than n
reverse(arr, n - d, n - 1); // Reverse the last d elements
reverse(arr, 0, n - d - 1); // Reverse the first n - d elements
reverse(arr, 0, n - 1); // Reverse the entire array
}10. Leaders in an array
For a given array find all the leader elements. You can display elements in any order.
I/P: arr = {7, 10, 4, 3, 6, 5, 2}
O/P: 10 6 5 2
A “leader” in an array is an element that is greater than or equal to all the elements to its right. For example, in the array [16, 17, 4, 3, 5, 2], the leaders are 17, 5, and 2. They are leaders because no elements to their right are larger than themselves. The rightmost element in the array will be always a leader because there is no element to its right.
In the case of ascending sorted array { 10, 20, 30 }, only the last element is the leader whereas in the case of descending sorted array like { 30, 20, 10 } every element is a leader. If the array contains duplicate elements then that duplicate element will not be considered.
public class Test {
public static void main(String[] args) {
int arr[] = { 7, 10, 4, 3, 6, 5, 2 };
leaders(arr);
}
private static void leaders(int[] arr) {
int n = arr.length, leader = arr[n - 1];
System.out.print(leader + " ");
for (int i = arr.length - 2; i >= 0; i--) {
if (arr[i] > leader) {
leader = arr[i];
System.out.print(leader + " ");
}
}
}
}11. Maximum Difference
Find the maximum value of arr[j] – arr[i] such that j > i.
I/P: arr = {2, 3, 10, 6, 4, 8, 1}; O/P: 8 (from 10 – 2)
I/P: arr = {7, 9, 5, 6, 3, 2}; O/P: 2 (from 9 – 7)
I/P: arr = {10, 20, 30}; O/P: 20 (from 30 – 10)
I/P: arr = {30, 10, 8, 2}; O/P: -2 (from 8 – 10)
If the array is ascending sorted like {10, 20, 30}, the result will be lastElement - firstElement. But the result will be negative if the array is sorted in descending order like {30, 10, 8, 2}.
public class Test {
public static void main(String[] args) {
int arr[] = { 2, 3, 10, 6, 4, 8, 1 };
System.out.println(maxDiff(arr));
}
// Naive solution
private static int maxDiff(int[] arr) {
int res = arr[1] - arr[0];
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i + 1; j < arr.length; j++) {
res = Math.max(res, arr[j] - arr[i]);
}
}
return res;
}
}Time complexity: θ(n2), Space complexity: θ(1)
Efficient Solution:- we consider every element of the array as j and also keep track of the minimum element so far.
public class Test {
public static void main(String[] args) {
int arr[] = { 2, 3, 10, 6, 4, 8, 1 };
System.out.println(maxDiff(arr));
}
private static int maxDiff(int[] arr) {
int res = arr[1] - arr[0];
int minVal = arr[0];
for (int j = 1; j < arr.length; j++) {
res = Math.max(res, arr[j] - minVal);
minVal = Math.min(minVal, arr[j]);
}
return res;
}
}For arr = { 2, 3, 10, 6, 4, 8, 1 };
res = arr[1] – arr[0] = 3 – 2 = 1
minVal = arr[0] = 2
Iteration j = 1
res = max(1, 3-2) = 1
minVal = min(2, 3) = 2
Iteration j = 2
res = max(1, 10-2) = 8
minVal = min(2, 10) = 2
Iteration j = 3
res = max(8, 6-2) = 8
minVal = min(2, 6) = 2
12. Frequencies in a sorted Array
I/P: arr = {10, 10, 10, 25, 30, 30};
O/P: 10=3, 25=1, 30=2
You may approach using HashMap. However, since the array is sorted, you can take advantage of that property to make your solution more efficient and concise. You can count the frequency of each element in a single pass without needing a HashMap. Also see:- Frequencies in an unsorted array
public class Test {
public static void main(String[] args) {
int[] arr = { 10, 10, 10, 25, 30, 30 };
frequencyInSortedArray(arr);
}
private static void frequencyInSortedArray(int[] arr) {
int count = 1, n = arr.length;
for (int i = 1; i < n; i++) {
if (arr[i] == arr[i - 1]) {
count++;
} else {
System.out.println(arr[i - 1] + ": " + count);
count = 1; // reset count for new element
}
}
// Print the count for the last element
System.out.println(arr[n - 1] + ": " + count);
}
}13. Stock Buy and Sell
The array contains the price of the stock in upcoming days. We have to buy the stock and sell it in upcoming days. Find the maximum profit. Stocks can’t be sold on the same day.
I/P: arr = {1, 5, 3, 8, 12}; O/P: 13
I/P: arr = {30, 20, 10}; O/P: 0
I/P: arr = {10, 20, 30}; O/P: 20
I/P: arr = {1, 5, 3, 1, 2, 8}; O/P: 11
For arr[] = {1, 5, 3, 8, 12} buy at 1 and sell at 5. Again buy at 3 and sell at 12. Total profit = (5-1) + (12-3) = 13
If prices are sorted in ascending order {10, 20, 30} then maximum profit can be achieved when buying on 1st day and selling on the last day. Similarly, if prices are sorted in descending order {30, 20, 10} then maximum profit = 0.
If the prices are going down then we will let them go down. Once the price reaches the bottom then we will buy the stock. When prices are going up we will let them go up. Once it reaches a peak then we will sell the stock. So, we will have to find the bottom and peak points.
We sell whenever we see a rise in the price. Consider prices {1, 5, 3, 8, 12} buy at 3, sell at 8, again sell 12 so it will give 12 – 3 = 9 (cumulative effect).
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 5, 3, 8, 12 };
int profit = 0;
for (int i = 1; i < arr.length; i++) {
if (arr[i] > arr[i - 1]) {
profit += arr[i] - arr[i - 1];
}
}
System.out.println(profit);
}
}14. Trapping Rain Water
This is one of the frequently asked questions in DSA. Given an array of n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after rain.
I/P: arr = {2, 0, 2}; O/P: 2
I/P: arr = {3, 0, 1, 2, 5}; O/P: 6
I/P: arr = {5, 0, 6, 2, 3}; O/P: 6
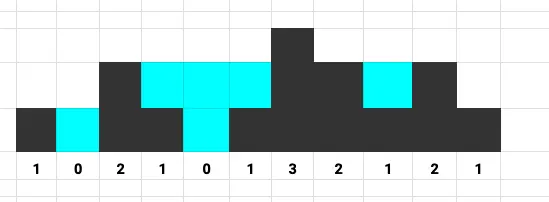
If the array is sorted either in ascending or descending then we can’t collect any water because there is nothing to stop the water, it will flow.
- Rightmost and leftmost bars can’t store the water, only middle ones can. Therefore iterate through i=1 to n-1 (considering 0-based index of the array).
- In the ith bar how much water we can store? It depends upon 3 things:- left highest bar, right highest bar, and ith bar width. If ith bar width is 0 then max water that can be stored at ith bar = min(leftMaxBar, rightMaxBar). Considering the ith bar width,
res[i] = min(leftMaxBar, rightMaxBar) - arr[i].
Efficient solution:- Pre-compute the left and right max bars.
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = { 5, 0, 6, 2, 3 };
int res = 0;
int[] lmax = new int[arr.length];
int[] rmax = new int[arr.length];
lmax[0] = arr[0];
for (int i = 1; i < lmax.length; i++) {
lmax[i] = Math.max(lmax[i - 1], arr[i]);
}
System.out.println(Arrays.toString(lmax));
rmax[arr.length - 1] = arr[arr.length - 1];
for (int i = arr.length - 2; i >= 0; i--) {
rmax[i] = Math.max(rmax[i + 1], arr[i]);
}
System.out.println(Arrays.toString(rmax));
for (int i = 0; i < arr.length; i++) {
res += (Math.min(lmax[i], rmax[i]) - arr[i]);
}
System.out.println(res);
}
}Time complexity: O(n), Space complexity: O(n).
15. Maximum Consecutive 1s
In the given array count the maximum consecutive 1s. Problem: 485. Extended Problem: 1004.
I/P: arr = {0, 1, 1, 0, 1, 0}; O/P: 2
I/P: arr = {1, 1, 1, 1}; O/P: 4
I/P: arr = {0, 0, 0}; O/P: 0
public class Test {
public static void main(String[] args) {
int arr[] = { 0, 1, 1, 0, 1, 0 };
int maxCount = 0;
int currentCount = 0;
for (int k : arr) {
if (k == 1) {
currentCount++;
maxCount = Math.max(maxCount, currentCount);
} else {
currentCount = 0;
}
}
System.out.println(maxCount);
}
}16. Maximum Length Even Odd Subarray
Find the maximum length of the subarray with alternating even odd elements.
I/P: {10, 12, 14, 7, 8}; O/P: 3
I/P: {7, 10, 13, 14}; O/P: 4
I/P: {10, 12, 8, 4}; O/P: 1
public class Test {
public static void main(String[] args) {
int arr[] = { 5, 10, 20, 6, 3, 8 };
System.out.println(maxOddEvenSubArray(arr));
}
private static int maxOddEvenSubArray(int[] arr) {
int maxCount = 1, current = 1;
for (int i = 1; i < arr.length; i++) {
int prevEle = arr[i - 1];
int currentEle = arr[i];
if (
((prevEle & 1) == 0 && (currentEle & 1) == 1) ||
((prevEle & 1) == 1 && (currentEle & 1) == 0)
) {
current++;
maxCount = Math.max(maxCount, current);
} else {
current = 1;
}
}
return maxCount;
}
}17. Kadane’s Algorithm
a. Maximum Sum Subarray
Given an array of integers, find the contiguous subarray (containing at least one number) that has the largest sum and return that sum.
What is a subarray? Subarray of {1, 2, 3} are {1}, {2}, {3}, {1, 2}, {2, 3} and {1, 2, 3}.
I/P: arr = {2, 3, -8, 7, -1, 2, 3}; O/P: 11 (from subarray {7, -1, 2, 3})
I/P: arr = {5, 8, 3}; O/P: 16 (from entire array)
I/P: arr = {-6, -1, -8}; O/P: -1 (from {-1})
Naive solution with time complexity O(n^2).
public class Test {
public static void main(String[] args) {
int arr[] = { 2, 3, -8, 7, -1, 2, 3 };
System.out.println(maxSumSubArray(arr));
}
private static int maxSumSubArray(int[] arr) {
int res = arr[0];
for (int i = 0; i < arr.length; i++) {
int curr = 0;
for (int j = i; j < arr.length; j++) {
curr = curr + arr[j];
res = Math.max(curr, res);
}
}
return res;
}
}Kadane’s Algorithm
Kadane’s Algorithm is a popular and efficient way to find the maximum sum subarray in linear time O(n). Traverse the array from left to right. For each ith element, find the max sum array that will end with the ith subarray. The overall result will be the maximum of these values.
The max sum sub array at i=1 is Max(arr[1], maxSum[0] + arr[1]).
Similarly at i = 2: max(arr[2], maxSum[1] + arr[2])
Hence, the max sum of the sub-array at i = max(arr[i], maxSum[i-1] + arr[i])
Find the largest element of this resultant array.
arr = { -5, 1, -2, 3, -1, 2, -2 };
maxSumArray = { -5, 1, -1, 3, 2, 4, 2 }; // max element = 4
public class Test {
public static void main(String[] args) {
int arr[] = { -5, 1, -2, 3, -1, 2, -2 };
System.out.println(maxSumSubArray(arr)); // 4
}
private static int maxSumSubArray(int[] arr) {
int res = arr[0];
int maxSum = arr[0];
for (int i = 1; i < arr.length; i++) {
maxSum = Math.max(arr[i], maxSum + arr[i]);
res = Math.max(res, maxSum);
}
return res;
}
}It also can be done as:-
public class Test {
public static void main(String[] args) {
int[] arr = { -2, -3, 4, -1, -2, 1, 5, -3 };
System.out.println(maxSubarraySum(arr));
}
private static int maxSubarraySum(int[] arr) {
int sum = 0, max = 0;
for (int k : arr) {
sum += k;
max = Math.max(max, sum);
if (sum < 0) {
sum = 0;
}
}
return max;
}
}If we want to show the subarray then:-
public class Test {
public static void main(String[] args) {
int[] arr = { -2, -3, 4, -1, -2, 1, 5, -3 };
System.out.println(maxSubarraySum(arr));
}
private static int maxSubarraySum(int[] arr) {
int sum = 0, max = 0, ansStart = -1, ansEnd = -1;
int start = 0;
for (int i = 0; i < arr.length; i++) {
if (sum == 0) {
start = i;
}
sum += arr[i];
if (sum > max) {
max = sum;
ansStart = start;
ansEnd = i;
}
if (sum < 0) {
sum = 0;
}
}
// subArray index
System.out.println("Subarray Index: [" + ansStart + ", " + ansEnd + "]");
return max;
}
}b. Minimum Sum Subarray
Given an array of integers, find the contiguous subarray (containing at least one number) which has the smallest sum and return that sum.
Array = {2, 3, -8, 7, -1, 2, 3}; O/P: -8
Array = {-6, -1, -8}; O/P: -15 from entire array
We can use an adaptation of Kadane’s Algorithm to find the minimum sum subarray. Instead of tracking the maximum sum subarray, we track the minimum sum subarray.
public class Test {
public static void main(String[] args) {
int arr[] = { 2, 3, -8, 7, -1, 2, 3 };
System.out.println(minSumSubarray(arr)); // -8
}
private static int minSumSubarray(int[] arr) {
int res = Integer.MAX_VALUE, minEnding = 0;
for (int k : arr) {
minEnding = Math.min(minEnding + k, k);
res = Math.min(res, minEnding);
}
return res;
}
}However, the same can be achieved using maxSumSubArray() also as follows:-
private static int minSumSubarray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
arr[i] = -arr[i];
}
return -maxSumSubArray(arr);
}c. Maximum Circular Subarray Sum
Consider array {10, 5, -5}. All circular subarrays are:-
Normal:- {10}, {5}, {-5}, {10, 5}, {5, -5}, {10, 5, -5}
Circular:- {5, -5, 10}, {-5, 10}, {-5, 10, 5}
Array = {10, 5, -5}; O/P: 15 from {10, 5}
Array = {5, -2, 3, 4}; O/P: 12 from {3, 4, 5}
Array = {2, 3, -4}; O/P: 5 from {2, 3}
Array = {8, -4, 3, -5, 4}; O/P: 12 from {4, 8}
Array = {-3, 4, 6, -2}; O/P: 10 from {4, 6}
Array = {-8, 7, 6}; O/P: 13 from {7, 6}
Array = {3, -4, 5, 6, -8, 7}; O/P: 17 from {7, 3, -4, 5, 6}
Naive Solution with time complexity O(n^2):- Consider every array element as the beginning element, and find out the maximum sum that can be obtained by considering this as the beginning element.
public class Test {
public static void main(String[] args) {
int arr[] = { 5, -2, 3, 4 };
System.out.println(maxCircularSum(arr));
}
private static int maxCircularSum(int[] arr) {
int n = arr.length;
int res = arr[0];
for (int i = 0; i < n; i++) {
int curr_max = arr[i];
int curr_sum = arr[i];
for (int j = 1; j < n; j++) {
int index = (i + j) % n;
curr_sum += arr[index];
curr_max = Math.max(curr_max, curr_sum);
}
res = Math.max(res, curr_max);
}
return res;
}
}Array = { 5, -2, 3, 4 };
i=0: curr_max = 10, res = 10
i=1: curr_max = 10
i=2: curr_max = 12, res = 12
i=3: curr_max = 10
Efficient Solution with time complexity O(n). Idea: Take the maximum of the following two:-
- Maximum sum of a normal subarray (Using Kadane’s algorithm)
- Maximum sum of a circular subarray
public class Test {
public static void main(String[] args) {
int arr[] = { 5, -2, 3, 4 };
System.out.println(maxCircularSum(arr)); // 12
}
private static int maxCircularSum(int[] arr) {
// Step 1: Find the maximum sum subarray in the linear array
int maxNormal = maxSumSubArray(arr);
// If all elements are negative, return the max element (maxNormal)
if (maxNormal < 0) {
return maxNormal;
}
int sumArr = 0; // total sum of array
// Invert the elements of the array to find the minimum sum subarray
for (int i = 0; i < arr.length; i++) {
sumArr += arr[i];
arr[i] = -arr[i];
}
// max sum for the inverted array (which is negative of min sum subarray)
int maxInverted = maxSumSubArray(arr);
int maxCircular = sumArr + maxInverted;
return Math.max(maxNormal, maxCircular);
}
private static int maxSumSubArray(int[] arr) {
int maxEnding = arr[0], res = arr[0];
for (int i = 1; i < arr.length; i++) {
maxEnding = Math.max(maxEnding + arr[i], arr[i]);
res = Math.max(res, maxEnding);
}
return res;
}
}18. Majority Element in an Array
An element in a given array is called majority if it exists more than n/2 times, where n is the length of the array.
I/P: arr = {8, 3, 4, 8, 8}; O/P: Any index of 8
I/P: arr = {3, 7, 4, 7, 7, 5}; O/P: No majority (-1)
I/P: arr = {20, 30, 40, 50, 50, 50, 50}; O/P: Any index of 50
You may use hashing (HashMap) but it will have time complexity O(n) and space complexity O(n). We can solve this through Boyer-Moore Voting Algorithm which ensures O(n) time complexity and O(1) space complexity.
Boyer-Moore Voting Algorithm
- Initialization: Start with the first element as the candidate and set a count to 1.
- Traverse the Array:
- If the next element is the same as the candidate, increment the count.
- If the next element is different, decrease the count.
- If the count reaches zero, update the candidate to the next element and reset the count to 1.
- Verification (Optional): After one pass, the candidate is the majority element. You can make a second pass to verify that it appears more than n/2 times if necessary. This part is optional, if the question mentions that the array must contain one majority element then this part is not required. The need for this part is only there if the array may not contain a majority element.
public class Test {
public static void main(String[] args) {
int arr[] = { 8, 8, 6, 6, 6, 4, 6 };
System.out.println(findMajority(arr)); // 3
}
private static int findMajority(int[] arr) {
int n = arr.length, count = 1, majorityIndex = 0;
// Part-1: find a candidate
for (int i = 1; i < n; i++) {
if (arr[i] == arr[majorityIndex]) {
count++;
} else {
count--;
}
if (count == 0) {
majorityIndex = i;
count = 1;
}
}
// Part-2: verify if the candidate is actually a majority
count = 0;
for (int k : arr) {
if (k == arr[majorityIndex])
count++;
}
return count >= n / 2 ? majorityIndex : -1;
}
}19. Minimum Group Filps to Make the same
We can flip either 0 or 1, but not both. Find the minimum number of group flips to make an array containing the same element. Print those ranges which will require a flip.
I/P: arr[ ] = {1, 1, 0, 0, 0, 1} O/P: 1 group flip; From 2 to 4
I/P: arr[ ] = {1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1}; O/P: 2 group flip; From 1 to 3, From 5 to 6
I/P: arr[ ] = {1, 1, 1}; O/P: 0; Already same element
I/P: arr[ ] = {0, 1}; O/P: 1 group flip; From 0 to 0 or From 1 to 1
Solution-1: Traverse the array and count the number of groups of 1’s and 0’s. If the number of 1’s group is less than the number of 0’s group then the minimum flip required is by 1’s group. Therefore again traverse the array and print indexes of 1’s in the array. It will require 2 traversals.
How it can be done in a single traversal?
Fact: there are only two possibilities:-
- Group count differs by one. Example:- 11000111001, 00110001100, 1111, 0000
- The group count are same. Example:- 0011100011, 1100011110
If the beginning and ending elements are the same then the group count differs by one. Whereas if the beginning and ending elements are different then the group count is the same.
We can get minimum flips only if we flip the second group in the array (starting from the beginning). The second group is the only group whose count will be either the same or less than its counterpart. Example:- 11000111001 here 0’s group is the second group, in 00110001100 1’s group is the second group.
Solution 2: Traverse the array, and start from the second element. If the current element and the previous element are the same then it is part of the previous group else it is part of the new group.
public class Test {
public static void main(String[] args) {
int arr[] = { 0, 0, 1, 1, 0, 0, 1, 1, 0 };
printGroups(arr);
}
private static void printGroups(int[] arr) {
for (int i = 1; i < arr.length; i++) {
if (arr[i - 1] != arr[i]) {
if (arr[i] != arr[0]) {
System.out.print("From " + i + " to ");
} else {
System.out.println(i - 1);
}
}
}
if (arr[arr.length - 1] != arr[0]) {
System.out.println(arr.length - 1);
}
}
}Output:-
From 2 to 3
From 6 to 7
20. Windows Sliding Techniques
a. Max Sum Subarray of size K
Given an array of integers and a number k, find the maximum sum of k consecutive elements. Problem
I/P: arr[ ] = { 1, 8, 30, -5, 20, 7 }; k = 3; O/P: 45
I/P: arr[ ] = { 5, -10, 6, 90, 3 }; k = 2; O/P: 96
Consider 1st window as index 0 to k-1, and calculate its sum. For 2nd window => 1st window sum + arr[k] – arr[0]. Similarly for 3rd window => 2nd window sum + arr[k+1] – arr[2], and so on. With this, we can find the sum of each window in a single iteration and the max sum in that iteration.
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 8, 30, -5, 20, 7 };
int k = 3;
System.out.println(maxSum(arr, k)); // 45
}
private static int maxSum(int[] arr, int k) {
int maxSum = 0, windowSum = 0;
for (int end = 0, start = 0; end < arr.length; end++) {
windowSum += arr[end];
if (end >= k - 1) {
maxSum = Math.max(maxSum, windowSum);
windowSum -= arr[start++];
}
}
return maxSum;
}
}Time complexity = O(n), Space complexity = O(1)
b. Sub array of size K with Given Sum Exist or Not
Assume we have sum=45, k=3, and arr[] = { 1, 8, 30, -5, 20, 7 }, then we have to find out whether is there any subarray exist or not whose sum of k consecutive elements is 45.
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 8, 30, -5, 20, 7 };
int k = 3, sum=45;
System.out.println(windowSumExist(arr, k, sum)); // true
}
private static boolean windowSumExist(int[] arr, int k, int sum) {
int windowSum = 0;
for (int end = 0, start = 0; end < arr.length; end++) {
windowSum += arr[end];
if (end >= k - 1) {
if(windowSum == sum) {
return true;
}
windowSum -= arr[start++];
}
}
return false;
}
}c. Sub array with Given Sum (Only positive elements)
Given an unsorted array of non-negative integers. Find if there is a subarray with given sum. Here k is not given. Note:- It is an array of non-negative numbers. Problem
I/P: arr[ ] = {1, 4, 20, 3, 10, 5}; sum = 33; O/P: Yes
I/P: arr[ ] = {1, 4, 0, 0, 3, 10, 5}; sum = 7; O/P: Yes
I/P: arr[ ] = {2, 4}; sum=3; O/P: No
Iterate through the array, take currentWindowSum=0. Keep adding elements to the current window. Whenever currentWindowSum > sum, start removing from the beginning element. We will get either smaller sum or equal sum. If the sum is equal then return true.
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 8, 30, -5, 20, 7 };
int sum = 45;
System.out.println(existSum(arr, sum)); // true
}
private static boolean existSum(int[] arr, int sum) {
int i = 0, j = 0, windowSum = 0, n = arr.length;
while (i < n && j < n) {
if (windowSum == sum) {
return true;
} else if (windowSum < sum) {
windowSum += arr[i++];
} else {
windowSum -= arr[j++];
}
}
return false;
}
}Time complexity = O(n)
If you want to return 1-based indexes of windows start and end point then:-
import java.util.ArrayList;
public class Test {
public static void main(String[] args) {
int arr[] = { 5, 1, 2, 3, 4 };
int sum = 10;
System.out.println(subarraySum(arr, sum)); // true
}
public static ArrayList<Integer> subarraySum(int[] arr, int sum) {
ArrayList<Integer> rs = new ArrayList<>();
if (sum == 0) {
return rs;
}
int windowSum = 0, start = 0, n = arr.length;
for (int end = 0; end < n; end++) {
windowSum += arr[end];
while (windowSum > sum && start < end) {
windowSum -= arr[start++];
}
if (windowSum == sum) {
rs.add(start + 1);
rs.add(end + 1);
return rs;
}
}
return rs;
}
}d. Sub Array With Give Sum (Both positive & negative elements)
In the previous problem consider array has both negative and positive numbers.
When an array contains both positive and negative elements then the previous solution won’t work. Example array = {4, 7, -3, 1, 2}, sum = 9. So the windows is {4, 7, -3, 1}. But if we try to use the above solution then 4+7 = 11, and 11>7 which will eliminate the 4 from the current window.
When the array contains both positive and negative numbers, the sliding window technique won’t work because adjusting the window size based on the sum comparison doesn’t account for the negative numbers properly.
Instead, we can use a HashMap to track the cumulative sum and check if the subarray with the given sum exists. See solution:- Subarray with given sum
Also see:-
e. N-bonacci Number
Fibonacci is 2-bonacci where every element is the sum of the previous 2 elements. Similarly, 3-bonacci means every element is the sum of the previous 3 elements. N-bonacci means every element is the sum of the previous N element.
Print first M N-bonacci number.
I/P: N = 3, M = 8
O/P: 0 0 1 1 2 4 7 13
I/P: N=4, M=10
O/P: 0 0 0 1 1 2 4 8 15 29
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
System.out.println(Arrays.toString(nBonacciNums(3, 8)));
System.out.println(Arrays.toString(nBonacciNums(4, 10)));
}
private static int[] nBonacciNums(int k, int n) {
int windowSum = 0;
int[] nums = new int[n];
nums[k - 1] = 1;
for (int i = 0; i < n; i++) {
if (i < k) {
windowSum += nums[i];
} else {
nums[i] = windowSum;
windowSum += (nums[i] - nums[i - k]);
}
}
return nums;
}
}Output:-
[0, 0, 1, 1, 2, 4, 7, 13]
[0, 0, 0, 1, 1, 2, 4, 8, 15, 29]
F. Count distinct elements in every window of size K
I/P: arr = {1, 2, 1, 3, 4, 3, 3}, k = 4
O/P: 3 4 3 2
Problem
We can solve this problem using hashing (HashMap) but it will have time complexity O(n * k). How can we optimize it in O(n)?
To solve this problem in O(n) time complexity, you can use a sliding window approach combined with a HashMap to track each element’s frequency within the current window.
Steps:-
- Create a frequency map of the first k items.
- Print the size of the frequency map.
- Traverse through the loop from i=k to n.
- Decrease frequency of arr[i – k].
- If the frequency of arr[i – k] becomes 0, remove it from the map.
- If arr[i] does not exist in the map, insert it or else increase its frequency in the map.
- Print the size of the map.
public class Test {
public static void main(String[] args) {
int arr[] = { 1, 2, 1, 3, 4, 3, 3 };
int k = 4;
countDistinctElements(arr, k); // 3 4 3 2
}
private static void countDistinctElements(int[] arr, int k) {
Map<Integer, Integer> unique = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (i >= k) {
System.out.print(unique.size() + " ");
// remove the element that is going out of the window
int ele = arr[i - k];
if (unique.get(ele) > 1) {
unique.put(ele, unique.get(ele) - 1);
} else {
unique.remove(ele);
}
}
unique.put(arr[i], unique.getOrDefault(arr[i], 0) + 1);
}
System.out.print(unique.size() + " ");
}
}21. Prefix sum
Given a fixed array and multiple queries of the following type on the array, how to efficiently perform these queries:-
I/P: array = {2, 8, 3, 9, 6, 5, 4};
Queries:- sum(0, 2), sum(1, 3), sum(2, 6). Here sum(0, 2) means the sum of array elements from index 0 to 2 (both inclusive).
O/P: 13 20 27
To solve this problem we can first find the prefix sum array, where we create an array of the same size, and ith element is the sum of the first i element of the original array.
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = { 2, 8, 3, 9, 6, 5, 4 };
int[] prefixSum = new int[arr.length];
prefixSum[0] = arr[0];
for (int i = 1; i < arr.length; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
}
System.out.println(Arrays.toString(prefixSum));
// [2, 10, 13, 22, 28, 33, 37]
}
}Now to find the sum(1, 3) we can use the prefixSum array as:- prefixSum[3] – prefixSum[0]; If the starting index is 0 like sum(0, 2) then we can return prefixSum[2].
public class Test {
public static void main(String[] args) {
int[] arr = { 2, 8, 3, 9, 6, 5, 4 };
int[] prefixSum = new int[arr.length];
prefixSum[0] = arr[0];
for (int i = 1; i < arr.length; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
}
System.out.println(sum(prefixSum, 0, 2)); // 13
System.out.println(sum(prefixSum, 1, 3)); // 20
System.out.println(sum(prefixSum, 2, 6)); // 27
}
private static int sum(int[] prefixSum, int i, int j) {
return i <= 0 ? prefixSum[j] : prefixSum[j] - prefixSum[i - 1];
}
}Time complexity O(n) and auxiliary space complexity O(n).
Also see:- Prefix Sum for 2D Array
a. Find Equilibrium Point
Given an array of integers, find if it has an equilibrium point? The equilibrium point is a point where all the left element sum is equal to the sum of all the right elements.
array={3, 4, 8, -9, 20, 6}; O/P: Yes (20); The sum of all elements right side of the element 20 and the sum of all left elements are equal.
array={4, 2, -2} O/P: Yes (4)
array={4, 2, 2} O/P: No
To solve this, we can find the prefixSum array and reversePrefixSum array (where the prefixSum array is calculated from the last index to the first index i.e. in reverse order. Then compare both arrays, if it has an equal element at any index then it has an equilibrium point.
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int[] arr = { 3, 4, 8, -9, 20, 6 };
System.out.println(containsEquilibriumPoint(arr));
}
private static boolean containsEquilibriumPoint(int[] arr) {
int[] prefixSum = new int[arr.length];
int[] revPrefixSum = new int[arr.length];
prefixSum[0] = arr[0];
for (int i = 1; i < arr.length; i++) {
prefixSum[i] = prefixSum[i - 1] + arr[i];
}
System.out.println(Arrays.toString(prefixSum));
revPrefixSum[arr.length - 1] = arr[arr.length - 1];
for (int i = arr.length - 2; i >= 0; i--) {
revPrefixSum[i] = revPrefixSum[i + 1] + arr[i];
}
System.out.println(Arrays.toString(revPrefixSum));
// compare both array
for (int i = 0; i < arr.length; i++) {
if (prefixSum[i] == revPrefixSum[i]) {
return true;
}
}
return false;
}
}Output:-
[3, 7, 15, 6, 26, 32]
[32, 29, 25, 17, 26, 6]
true
The above program has time complexity O(n) and auxiliary space O(n). We can optimize it without creating arrays. Instead, find the sum of all array elements from left to right then start iterating from right to left. In this way, it will have auxiliary space O(1).
public class Test {
public static void main(String[] args) {
int[] arr = { 3, 4, 8, -9, 20, 6 };
System.out.println(containsEquilibriumPoint(arr));
}
private static int containsEquilibriumPoint(int[] arr) {
int prefixSum = 0;
for (int k : arr) {
prefixSum += k;
}
int suffixSum = 0;
for (int i = arr.length - 1; i >= 0; i--) {
prefixSum -= arr[i];
if (prefixSum == suffixSum) {
return arr[i];
}
suffixSum += arr[i];
}
return -1;
}
}Time complexity O(n) and auxiliary space O(1).
b. Range Update Queries on Array (Scanline Algorithm)
Given an array of integers, perform multiple update queries. Each query specifies a range and an increment value. For each query, increase every element in the specified range by the given value. After performing all queries, print the resultant array.
Input:-
- An integer 𝑛 represents the size of the array.
- An array of integers of size 𝑛.
- An integer 𝑄 representing the number of queries.
- 𝑄 queries, each having three integers 𝐿, 𝑅, and 𝑥:
- 𝐿: Starting index of the range (0-based).
- 𝑅: Ending index of the range (0-based).
- 𝑥: The value by which elements within the range are to be incremented.
n = 5
Array = {2, 3, 2, 3, 5}
𝑄 queries:
(0, 2, 1)
(1, 4, 2)
(3, 3, 3)
Output:- {3, 6, 5, 8, 7}
Initial array = {2, 3, 2, 3, 5}
After query (0, 2, 1), array = {3, 4, 3, 3, 5}
After query (1, 4, 2), array = {3, 6, 5, 5, 7}
After query (3, 3, 3), array = {3, 6, 5, 8, 7}
Scanline Algorithm
The technique we used with the difference array (or delta array) to handle range updates efficiently is often referred to as a form of scanline algorithm. Originally, scanline algorithms are widely used in computer graphics and computational geometry. They process objects line by line (or scanline by scanline) to determine positions or intersections.
In Context of Range Updates: The difference array approach can be considered a type of scanline algorithm for range updates in arrays. It involves marking the start and end of an interval (or range) and then processing these marks to apply the increments efficiently.
This technique involves maintaining a difference array to handle range increments efficiently.
- Initialize Difference Array: Create a difference array diff of size n + 1 to handle boundary conditions with all elements 0 (default).
- Process Queries: For each query, update the start index L by adding x and update the index R + 1 by subtracting x (if R + 1 is within bounds).
- Compute Resultant Array: Iterate through the difference array to compute the prefix sum, which gives the final array.
- Add the original array and prefix-sum array. Ignore the last element of the prefix sum array.
Example:-
Array = {2, 3, 2, 3, 5}
𝑄 queries:
(0, 2, 1)
(1, 4, 2)
(3, 3, 3)
Difference array = {0, 0, 0, 0, 0, 0}
For 1st query (0, 2, 1), diff array = {1, 0, 0, -1, 0, 0}
For 2nd query (1, 4, 2), diff array = {1, 2, 0, -1, 0, -2}
For 3rd query (3, 3, 3), diff array = {1, 2, 0, 2, -3, -2}
The prefix sum of diff array = {1, 3, 3, 5, 2, 0}
Add the original array and prefix sum by ignoring the (n+1)th index =
{2, 3, 2, 3, 5} + {1, 3, 3, 5, 2} = {3, 6, 5, 8, 7}
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int n = 5;
int[] array = { 2, 3, 2, 3, 5 };
// Queries: {L, R, x}
int[][] queries = {
{0, 2, 1},
{1, 4, 2},
{3, 3, 3}
};
applyRangeUpdateQueries(array, n, queries);
System.out.println(Arrays.toString(array));
// [3, 6, 5, 8, 7]
}
private static void applyRangeUpdateQueries(int[] array, int n, int[][] queries) {
int[] diff = new int[n + 1];
for (int[] query : queries) {
int l = query[0];
int r = query[1];
int x = query[2];
diff[l] += x;
diff[r + 1] -= x;
}
// prefix sum
for (int i = 1; i < diff.length; i++) {
diff[i] = diff[i - 1] + diff[i];
}
// add diff array to original array
for (int i = 0; i < array.length; i++) {
array[i] += diff[i];
}
}
}Also see:- Range Update Queries on a 2D Array
c. Maximum appearing element in a set of ranges
You have a set of ranges, and you need to find the element that appears most of the time within those ranges.
Given:-
- Start Points (S/p): Array of integers representing the starting points of ranges.
- End Points (R/p): Array of integers representing the endpoints of ranges.
Output: The element that appears the most within these ranges.
Example:-
Given ranges:
S/p = {1, 2, 5, 15}
R/p = {5, 8, 7, 18}
The ranges are: [1, 5], [2, 8], [5, 7], [15, 18]
Based on the given ranges, it contains the following elements:-
[1, 5]:- {1, 2, 3, 4, 5}
[2, 8]:- {2, 3, 4, 5, 6, 7, 8}
[5, 7]:- {5, 6, 7}
[15, 18]:- {15, 16, 17, 18}
In these elements, 5 often appear (3 times). Hence output is 5.
The naive solution can be to initialize all ranges and use HashMap to count the frequency. It will have time complexity O(n*m) and space complexity O(n).
If the range never goes beyond 1000 elements then we can optimize using the scanline algorithm (difference array approach):-
- Difference Array: Create a difference array diff of size maxRange + 2 (or simpliy 1000) to account for the boundary conditions.
- Process Ranges: For each range defined by startPoints and endPoints, increment the start index and decrement the position right after the end index in the difference array.
- Compute Frequency: Compute the prefix sum of the difference array to get the frequency of appearances for each element. Store the prefix sum results in an array freq.
- Find Maximum Frequency: Iterate through the freq array to find the element with the maximum frequency of appearances.
public class Test {
public static void main(String[] args) {
int[] l = { 1, 2, 3 };
int[] r = { 3, 5, 7 };
System.out.println(max(l, r)); // 3
}
private static int max(int[] l, int[] r) {
// Initialize the difference array of size 1000
// (assuming the range never goes beyond 1000)
int[] diff = new int[1000];
for (int i = 0; i < l.length; i++) {
// Increment the start index of the range
diff[l[i]]++;
// Decrement the element right after the end index of the range
diff[r[i] + 1]--;
}
int max = diff[0], res = 0;
// prefix sum
for (int i = 1; i < diff.length; i++) {
diff[i] += diff[i - 1];
// Update the maximum frequency and the result element
// if the current frequency is higher
if (max < diff[i]) {
max = diff[i];
res = i;
}
}
return res;
}
}d. Array Divided into 3 Parts with Equal Sum
Check if a given array can be divided into three parts with equal sum. Example:- {0, 2, 1, -1, 1, -1, 1, 0, 1, 1}.
Steps to solve the problem:-
- Calculate Total Sum: If the total sum is not divisible by 3, it’s impossible.
- Find Subarray sums: Traverse the array to check if we can find three subarrays with the target sum.
public class Test {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 0, 3 }; // total sum: 9
System.out.println(equalThreeSubArrayExist(arr));
}
private static boolean equalThreeSubArrayExist(int[] arr) {
int totalSum = 0;
for (int k : arr) {
totalSum += k;
}
if (totalSum % 3 != 0) {
return false;
}
int targetSum = totalSum / 3;
int currentSum = 0;
int count = 0;
for (int k : arr) {
currentSum += k;
if (currentSum == targetSum) {
count++;
currentSum = 0;
}
}
return count >= 3;
}
}If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!