Matrix DSA

Matrix DSA | Let us see the problems related to multidimensional arrays or Matrices. We will discuss how the sorting can be done, how different patterns can be displayed, and how the power can be calculated.

Table of Contents

• Print Matrix in Snake Pattern
• Print Boundary Elements of Matrix
• Transpose of a Matrix
• Rotate the Matrix Anti Clockwise by 90 Degrees
• Rotate the Matrix Clockwise by 90 Degrees
• Spiral Traversal of Matrix
• Search in Row wise and Column wise Sorted Matrix
• The median of a Row Wise Sorted Matrix
• Others
  • Binary Exponentiation of Matrix
    • Fibonacci Number Using Matrix Exponentiation
    • Tribonacci Number Using Matrix Exponentiation
    • Two Recurrence Problems Using Matrix Exponentiation
  • 2D Prefix Sum
  • Range Sum Queries in 2D Matrices
  • Range Update Queries on a 2D Array

Multidimensional Arrays in Java

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] arr = { { 1, 2, 3, 8, 9 }, { 4, 5, 6 } };
        System.out.println(Arrays.deepToString(arr));

        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                System.out.println(arr[i][j] + " ");
            }
        }
    }
}

Since it is an array of arrays therefore it is mandatory that arrays are stored in contiguous locations. It means array for array[0], and array for array[1] may stored in two different locations.

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int m = 2, n = 3;
        int[][] arr = new int[m][n];
        System.out.println(Arrays.deepToString(arr)); 
        // [[0, 0, 0], [0, 0, 0]]

        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                arr[i][j] = j;
            }
        }
        System.out.println(Arrays.deepToString(arr)); 
        // [[0, 1, 2], [0, 1, 2]]
    }
}

Example of Jagged Array (having different row sizes) of user-specified sizes

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int m = 3;
        int[][] arr = new int[m][]; // column size is dynamic

        for (int i = 0; i < arr.length; i++) {
            arr[i] = new int[i + 1];
            for (int j = 0; j < arr[i].length; j++) {
                arr[i][j] = i;
            }
        }
        System.out.println(Arrays.deepToString(arr)); 
        // [[0], [1, 1], [2, 2, 2]]
    }
}

Passing 2D array as an argument in Java

public class Test {
    public static void main(String[] args) {
        int[][] arr = { { 1, 2, 3, 8, 9 }, { 4, 5, 6 } };
        print(arr);
    }

    private static void print(int[][] arr) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                System.out.print(arr[i][j] + " ");
            }
            System.out.println();
        }
    }
}

Print Matrix in Snake Pattern

Given a 2D matrix, traverse the matrix in a snake-like pattern and return the elements in the order they are visited. Example-1:-

int[][] matrix = {
    {1, 2, 3, 4},
    {5, 6, 7, 8},
    {9, 10, 11, 12},
    {13, 14, 15, 16}
};

Output: 1 2 3 4 8 7 6 5 9 10 11 12 16 15 14 13

Example-2:-

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9},
    {10, 11, 12}
};

Output: 1 2 3 6 5 4 7 8 9 12 11 10

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { 
                { 1, 2, 3, 4 }, 
                { 5, 6, 7, 8 }, 
                { 9, 10, 11, 12 }, 
                { 13, 14, 15, 16 } 
           };
        snakePattern(matrix); // 1 2 3 4 8 7 6 5 9 10 11 12 16 15 14 13 
    }

    private static void snakePattern(int[][] matrix) {
        for (int i = 0; i < matrix.length; i++) {
            if (i % 2 == 0) {
                for (int j = 0; j < matrix[i].length; j++) {
                    System.out.print(matrix[i][j] + " ");
                }
            } else {
                for (int j = matrix[i].length - 1; j >= 0; j--) {
                    System.out.print(matrix[i][j] + " ");
                }
            }
        }
    }
}

Print Boundary Elements of Matrix

Given a 2D matrix, print all the boundary elements of the matrix in a single traversal. Similar Problem Example-1:-

int[][] matrix = {
    {1, 2, 3, 4},
    {5, 6, 7, 8},
    {9, 10, 11, 12},
    {13, 14, 15, 16}
};

Output: 1 2 3 4 8 12 16 15 14 13 9 5

Example-2:-

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9},
    {10, 11, 12}
};

Output: 1 2 3 6 9 12 11 10 7 4

Example-3: 1 2 3 4
Output:- 1 2 3 4

Example-4:-

int[][] matrix = {
    {1, 2},
    {3, 4},
    {5, 6}
};

Output:- 1 2 4 6 5 3

public class Test {
    public static void main(String[] args) {
        int[][] matrix = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12},
                {13, 14, 15, 16}
            };
        int[][] matrix1 = {{1, 2, 3, 4}};
        int[][] matrix2 = {
                {1},
                {2},
                {3},
                {4}
            };
        boundaryTraversal(matrix2);  
    }

    private static void boundaryTraversal(int[][] matrix) {
        int rows = matrix.length, cols = matrix[0].length;
        // print top row
        for (int j = 0; j < cols; j++) {
            System.out.print(matrix[0][j] + " ");
        }

        // print right column
        for (int i = 1; i < rows - 1; i++) {
            System.out.print(matrix[i][matrix[i].length - 1] + " ");
        }

        // print bottom row, if rows > 1
        if (rows > 1) {
            for (int j = matrix[rows - 1].length - 1; j >= 0; j--) {
                System.out.print(matrix[rows - 1][j] + " ");
            }
        }

        // print left column, if matrix has more than one column
        if(cols > 1) {
            for (int i = rows - 2; i > 0; i--) {
                System.out.print(matrix[i][0] + " ");
            }
        }
    }
}

Transpose of a Matrix

Given a 2D square matrix (number of rows = number of cols), transpose the matrix. The transpose of a matrix is obtained by swapping rows with columns, i.e., the element at position (i, j) in the original matrix will be at position (j, i) in the transposed matrix. The rows get converted into the column, and the column gets converted into the rows. Problem: 867. Example-1:-

Input:

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

Output:-

int[][] transposed = {
    {1, 4, 7},
    {2, 5, 8},
    {3, 6, 9}
};

Matrix = [ [1,2,3],[4,5,6] ]
Transposed = [ [1,4],[2,5],[3,6] ]

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix1 = {
            {1, 2, 3},
            {4, 5, 6}
        };
        
        int[][] matrix2 = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
        };
        
        System.out.println(Arrays.deepToString(transpose(matrix1))); 
        // Output: [[1, 4], [2, 5], [3, 6]]
        System.out.println(Arrays.deepToString(transpose(matrix2))); 
        // Output: [[1, 4, 7], [2, 5, 8], [3, 6, 9]]
    }

    public static int[][] transpose(int[][] matrix) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        int[][] transposedMatrix = new int[cols][rows];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                transposedMatrix[j][i] = matrix[i][j];
            }
        }

        return transposedMatrix;
    }
}

If it is a square matrix then we only need swapping. In transpose diagonal elements remain the same, and the lower half (below the diagonal) is swapped with the upper half.

private static void transpose(int[][] matrix) {
    int rows = matrix.length, cols = matrix[0].length;
    for (int i = 0; i < rows; i++) {
        for (int j = i + 1; j < cols; j++) {
            // swap
            int temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
}

Rotate the Matrix Anti Clockwise by 90 Degrees

Given a square matrix, rotate the matrix 90 degrees anticlockwise. The rotation should be done in place without using any extra space for another matrix. Example:-

Input:-

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

Output:-

int[][] rotated = {
    {3, 6, 9},
    {2, 5, 8},
    {1, 4, 7}
};

1. Transpose the Matrix: Swap the elements across the main diagonal.
2. Reverse Rows: Reverse the order of elements in each row.

The transpose converts rows into columns. So the first row becomes the first column, and the second row becomes the second column. Example:-

Original matrix

1 2 3
4 5 6
7 8 9

After transpose

1 4 7
2 5 8
3 6 9

Now, reversing the row positions can give us the desired result. Matrix after reversing the rows:-

3 6 9
2 5 8
1 4 7

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
        rotate90DAntiClockwise(matrix);
        System.out.println(Arrays.deepToString(matrix));
    }

    private static void rotate90DAntiClockwise(int[][] matrix) {
        int n = matrix.length;
        transpose(matrix, n);
        reverseRows(matrix, n);
    }

    private static void transpose(int[][] matrix, int n) {
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }

    private static void reverseRows(int[][] matrix, int n) {
        for (int i = 0, j = n - 1; i < j; i++, j--) {
            int[] temp = matrix[i];
            matrix[i] = matrix[j];
            matrix[j] = temp;
        }
    }
}

Rotate the Matrix Clockwise by 90 Degrees

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise). Problem: 48

You have to rotate the image in place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

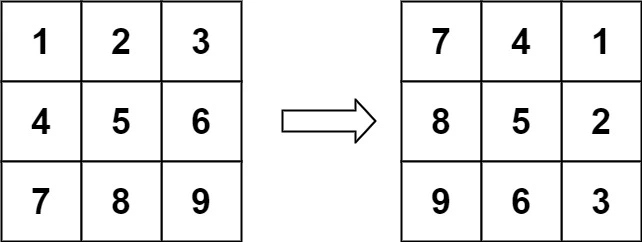
1. Transpose the Matrix: Swap the elements across the main diagonal.
2. Reverse Columns: Reverse the order of elements in each column.

Original matrix

1 2 3
4 5 6
7 8 9

After transpose

1 4 7
2 5 8
3 6 9

Now, reversing the column positions can give us the desired result. Matrix after reversing the columns:-

7 4 1
8 5 2
9 6 3

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
        rotate90DClockwise(matrix);
        System.out.println(Arrays.deepToString(matrix));
    }

    private static void rotate90DClockwise(int[][] matrix) {
        int n = matrix.length;
        transpose(matrix, n);
        reverseColumns(matrix, n);
    }

    private static void transpose(int[][] matrix, int n) {
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }

    private static void reverseColumns(int[][] matrix, int n) {
        for (int i = 0; i < n; i++) {
            for (int j = 0, k = n - 1; j < k; j++, k--) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][k];
                matrix[i][k] = temp;
            }
        }
    }
}

Spiral Traversal of Matrix

Given a 2D matrix, print the elements in a spiral order starting from the top-left corner of the matrix and moving inwards. Problem:- 54

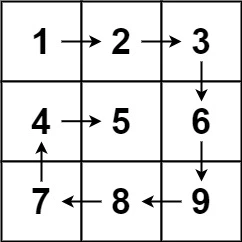
int[][] matrix = {
    {1, 2, 3, 4},
    {5, 6, 7, 8},
    {9, 10, 11, 12},
    {13, 14, 15, 16}
};

Output: 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10

Steps:-

1. Initialize Boundaries:

• Top Boundary (top): Starts at the first row, 0.
• Bottom Boundary (bottom): Starts at the last row, n-1.
• Left Boundary (left): Starts at the first column, 0.
• Right Boundary (right): Starts at the last column, m-1.

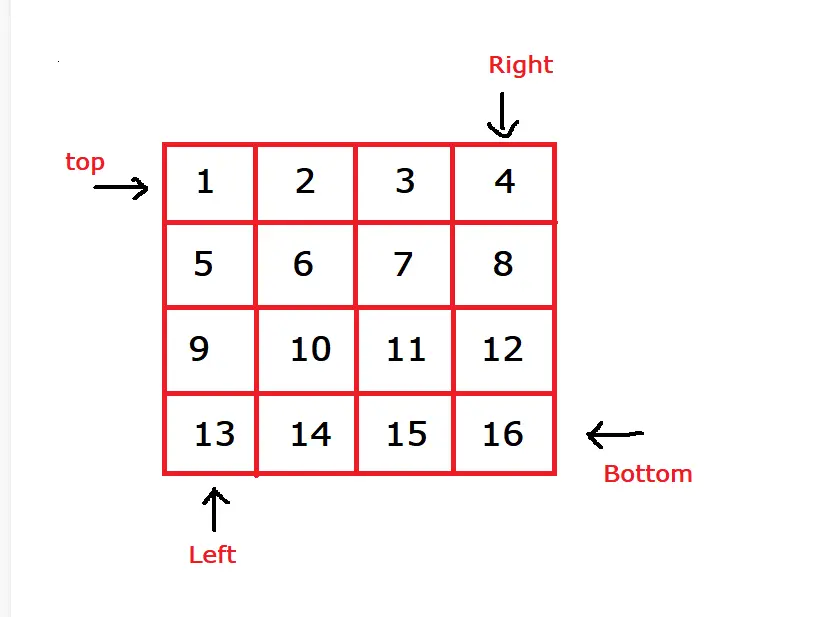
2. Traverse in Spiral Order:

• Left to Right: Traverse the elements in the top boundary row from left to right. Move the top boundary down by incrementing it.
• Top to Bottom: Traverse the elements in the right boundary column from top to bottom. Move the right boundary left by decrementing it.
• Right to Left: Traverse the elements in the bottom boundary row from right to left. Move the bottom boundary up by decrementing it.
• Bottom to Top: Traverse the elements in the left boundary column from bottom to top. Move the left boundary right by incrementing it.
• Repeat these steps until all boundaries overlap.

public class Test {
    public static void main(String[] args) {
        int[][] matrix = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12},
                {13, 14, 15, 16}
            };
        printSpiral(matrix);
    }

    private static void printSpiral(int[][] matrix) {
        int top = 0, left = 0, bottom = matrix.length - 1;
        int right = matrix[0].length - 1;

        while (top <= bottom && left <= right) {
            // top row
            for (int i = left; i <= right; i++) {
                System.out.print(matrix[top][i] + " ");
            }
            top++;

            // right column
            for (int i = top; i <= bottom; i++) {
                System.out.print(matrix[i][right] + " ");
            }
            right--;

            // bottom row (reverse order)
            if (top <= bottom) {
                for (int i = right; i >= left; i--) {
                    System.out.print(matrix[bottom][i] + " ");
                }
                bottom--;
            }

            // left column (reverse order)
            if (left <= right) {
                for (int i = bottom; i >= top; i--) {
                    System.out.print(matrix[i][left] + " ");
                }
                left++;
            }
        }
    }
}

Time Complexity: O(r * c) where r is the number of rows, and c is the number of columns.

Search in Row wise and Column wise Sorted Matrix

Given an n x m matrix where each row and each column is sorted in ascending order, find a given target element. The goal is to locate the element efficiently, ideally in O(n + m) time complexity. Problem: 240, 74. Example-1:-

int[][] matrix = {
    {10, 20, 30, 40},
    {15, 25, 35, 45},
    {27, 29, 37, 48},
    {32, 33, 39, 50}
};
int target = 29;

Output: Found at (2, 1)

Example-2:-

int[][] matrix = {
    {1, 4, 7, 11},
    {2, 5, 8, 12},
    {3, 6, 9, 16},
    {10, 13, 14, 17}
};
int target = 15;

Output: -1

A naive solution is to iterate all the elements of the matrix and compare it with the target element. If it matches then display the index of row and column. The time complexity will be O(m * n) where m is the number of rows, and n is the number of columns.

Steps for an efficient solution O(m + n):-

• Begin from the top right corner.
• If x is same, print position and return.
• If x is smaller, move left (reduce column).
• If x is greater, move down (increase row).
• Repeat the above steps

public class Test {
    public static void main(String[] args) {
        int[][] matrix = {
                {10, 20, 30, 40},
                {15, 25, 35, 45},
                {27, 29, 37, 48},
                {32, 33, 39, 50}
            };
        int target = 29;
        System.out.println(search(matrix, target));
    }

    private static boolean search(int[][] matrix, int x) {
        int r = matrix.length, c = matrix[0].length;
        // corner case
        if (x < matrix[0][0] || x > matrix[r - 1][c - 1]) {
            return false;
        }

        int i = 0, j = c - 1;
        while (i < r && j >= 0) {
            if (matrix[i][j] == x) {
                System.out.println("Found at (" + i + ", " + j + ")");
                return true;
            } else if (matrix[i][j] > x) {
                j--; // move left
            } else {
                i++; // move down
            }
        }
        return false;
    }
}

The median of a Row Wise Sorted Matrix

Given a row-wise sorted m * n matrix (odd-sized), find the median of the matrix. The median is the middle element in a sorted, 1D representation of the matrix. Problem

Assumption:-

• Matrix is of odd sized.
• It has all distinct elements.

Example-1:-

int[][] matrix = {
    {1, 6, 10},
    {2, 5, 7},
    {3, 4, 9}
};

Output: 6 (The sorted 1D representation of the matrix is [1, 2, 4, 5, 6, 7, 8, 9, 10]. The median is the middle element 6)

Naive solution:-

• Put all elements in an array. It will take O(m * n).
• Sort the array. It will take O(m * n log m * n).
• Return the middle element from the sorted array.
• The overall time complexity will be O(m * n log m * n).

We can achieve an efficient solution using binary search. The time complexity will be O( m * log(maximumElement – minimumElement) * log n).

We will first find the maximum and minimum elements in the matrix. Some facts:-

• The maximum element will be always present in the last column.
• The minimum element will be always present in the first column.

Then we will use the binary search to find the mid element and then find the position of this mid element.

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 6, 10 }, { 2, 5, 7 }, { 3, 4, 9 } };
        System.out.println(median(matrix));
    }

    private static int median(int[][] matrix) {
        int r = matrix.length, c = matrix[0].length;
        int min = matrix[0][0], max = matrix[0][c - 1];
        for (int i = 1; i < r; i++) {
            min = Math.min(min, matrix[i][0]);
            max = Math.max(max, matrix[i][c - 1]);
        }
        int medPos = (r * c + 1) / 2;
        while (min < max) {
            int mid = (min + max) / 2, midPos = 0;
            for (int i = 0; i < r; i++) {
                int pos = Arrays.binarySearch(matrix[i], mid) + 1;
                midPos += Math.abs(pos);
            }
            if (midPos < medPos) {
                min = mid + 1;
            } else {
                max = mid;
            }
        }
        return min;
    }
}

You can also consider this case:- If the total number of elements is even, the median is the average of the two middle elements.

int[][] matrix = {
    {1, 2, 3, 4},
    {5, 6, 7, 8},
    {9, 10, 11, 12},
    {13, 14, 15, 16}
};

Output: 8.5 (The sorted 1D representation of the matrix is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]. The median is the average of the middle elements 8 and 9, i.e., (8 + 9) / 2 = 8.5)

Others

Binary Exponentiation of Matrix

Given an n x n matrix and an integer exponent k, your task is to compute the matrix raised to the power of k using binary exponentiation. Binary exponentiation is a method that reduces the time complexity of exponentiation to O(log k), making it efficient for large values of k. Example:-

int[][] matrix = {
    {1, 1},
    {1, 0}
};
int exponent = 5;

Result:-

int[][] result = {
    {8, 5},
    {5, 3}
};

Example-2:-

int[][] matrix = {
    {2, 0},
    {1, 3}
};
int exponent = 3;

Result:-

int[][] result = {
    {8, 0},
    {3, 27}
};

The solution is based on the Binary Exponentiation of a number. See here:- Binary Exponentiation of a number

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 1 }, { 1, 0 } };
        int exponent = 5;
        // int[][] matrix = { {2, 0}, {1, 3} }; int exponent = 3;
        int[][] result = matrixPower(matrix, exponent);
        System.out.println(Arrays.deepToString(result));
    }

    private static int[][] matrixPower(int[][] matrix, int exp) {
        int n = matrix.length;
        int[][] result = new int[n][n];

        // Initialize matrix as identity matrix
        for (int i = 0; i < n; i++) {
            result[i][i] = 1;
        }

        while (exp > 0) {
            if ((exp & 1) == 1) {
                result = multiplyMatrices(result, matrix);
            }
            matrix = multiplyMatrices(matrix, matrix);
            exp >>= 1;
        }

        return result;
    }

    private static int[][] multiplyMatrices(int[][] a, int[][] b) {
        int n = a.length;
        int[][] result = new int[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += a[i][k] * b[k][j];
                }
            }
        }
        return result;
    }
}

Fibonacci Number Using Matrix Exponentiation

Using matrix exponentiation to find the n-th Fibonacci number is a highly efficient method that reduces the time complexity to O(log n). It is based on the previous Binary Exponentiation of the Matrix problem.

⎡ F(n)   ⎤   =   ⎡ 1  1 ⎤ ^ n   ×   ⎡ F(1) ⎤
⎣ F(n-1) ⎦       ⎣ 1  0 ⎦           ⎣ F(0) ⎦
        

A = ⎡ 1  1 ⎤
    ⎣ 1  0 ⎦
        

public class Test {
    public static void main(String[] args) {
        int n = 10;
        System.out.println(fib(n)); // 55
    }

    private static long fib(int n) {
        if (n == 0)
            return 0;
        if (n == 1 || n == 2)
            return 1;

        long[][] result = { { 1, 0 }, { 0, 1 } }; // identity matrix
        long[][] base = { { 1, 1 }, { 1, 0 } };

        n = n - 1;
        while (n > 0) {
            if ((n & 1) == 1) {
                result = multiplyMatrices(result, base);
            }
            base = multiplyMatrices(base, base);
            n >>= 1;
        }

        return result[0][0];
    }

    private static long[][] multiplyMatrices(long[][] a, long[][] b) {
        int n = a.length;
        long[][] result = new long[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += a[i][k] * b[k][j];
                }
            }
        }
        return result;
    }
}

Tribonacci Number Using Matrix Exponentiation

The Tribonacci sequence is similar to the Fibonacci sequence, but instead of starting with two predetermined terms and each term being the sum of the two preceding ones, the Tribonacci sequence starts with three predetermined terms and each term is the sum of the three preceding ones.

Given an integer n, return the n-th Tribonacci number. The Tribonacci sequence Tn is defined as follows:-

• T0 = 0, T1 = 1, T2 = 1
• Tn = Tn-1 + Tn-2 + Tn-3 for n >= 3

Input: n = 4
Output: 4
Explanation: T0 = 0, T1 = 1, T2 = 1, T3 = 2, T4 = 4

Input: n = 10
Output: 149
Explanation: The first 11 terms of the Tribonacci sequence are: 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149

We can apply binary exponentiation to the Tribonacci sequence as well! The concept is similar to the Fibonacci matrix exponentiation but with a 3×3 matrix due to the nature of Tribonacci numbers.

The Tribonacci sequence can be represented using the following matrix:-

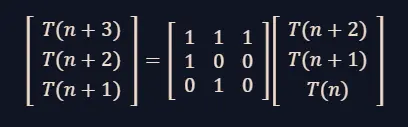
To find the n-th Tribonacci number, we need to raise this transformation matrix to the power of (𝑛 – 2) and multiply it by the initial vector.

At the end:-

[a b c] [T2]
[d e f] [T1]
[g h i] [T0]

The result will be a*T2 + b*T1 + c*T0.

public class Test {
    public static void main(String[] args) {
        int n = 10;
        System.out.println(fib(n)); // 149
    }

    private static long fib(int n) {
        if (n == 0)
            return 0;
        if (n == 1 || n == 2)
            return 1;

        // identity matrix
        long[][] result = { { 1, 0, 0 }, { 0, 1, 0 }, { 0, 0, 1 } };
        long[][] base = { { 1, 1, 1 }, { 1, 0, 0 }, { 0, 1, 0 } };

        n = n - 2;
        while (n > 0) {
            if ((n & 1) == 1) {
                result = multiplyMatrices(result, base);
            }
            base = multiplyMatrices(base, base);
            n >>= 1;
        }

        // The first element of the resulting matrix gives the nth Tribonacci number
        return result[0][0] * 1 + result[0][1] * 1 + result[0][2] * 0;
    }

    private static long[][] multiplyMatrices(long[][] a, long[][] b) {
        int n = a.length;
        long[][] result = new long[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += a[i][k] * b[k][j];
                }
            }
        }
        return result;
    }
}

Time complexity O(log n).

How to construct the base pattern?
For any recurrence relation of the form:-
T_n = a*T_n-1 + b*T_n-2 + c*T_n-3

The base matrix will be:-

[ a b c ]
[ 1 0 0 ]
[ 0 1 0 ]

Example-1:- T_n = 3*T_n-1 + 2*T_n-2 + T_n-3
The base matrix will be:-

[ 3 2 1 ]
[ 1 0 0 ]
[ 0 1 0 ]

And it should return:- result[0][0] * 3 + result[0][1] * 2 + result[0][2];

Example-2:- T_n = 2*T_n-1 + 1*T_n-2 – 2*T_n-3
The base matrix will be:-

[ 2 1 -2 ]
[ 1 0 0 ]
[ 0 1 0 ]

And it should return:- result[0][0] * 2 + result[0][1] – 2 * result[0][2];

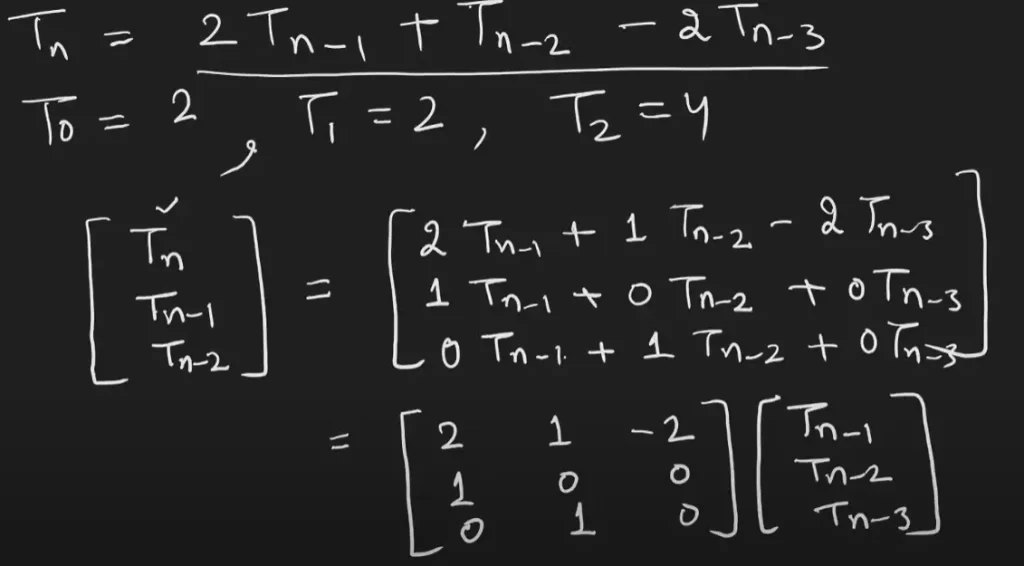
Two Recurrence Problems Using Matrix Exponentiation

What if we have recurrence where terms are in 2 recurrence relation? One recursive formula is dependent on another. Example:-

F_n = 2*F_n-1 – 3*F_n-2 + G_n
G_n = 5*G_n-1 + 4*G_n-2

In these cases, the matrix will have 4 terms (2 for F_n and 2 for G_n). See more:- https://www.youtube.com/watch?v=h41l3pJu6a8

2D Prefix Sum

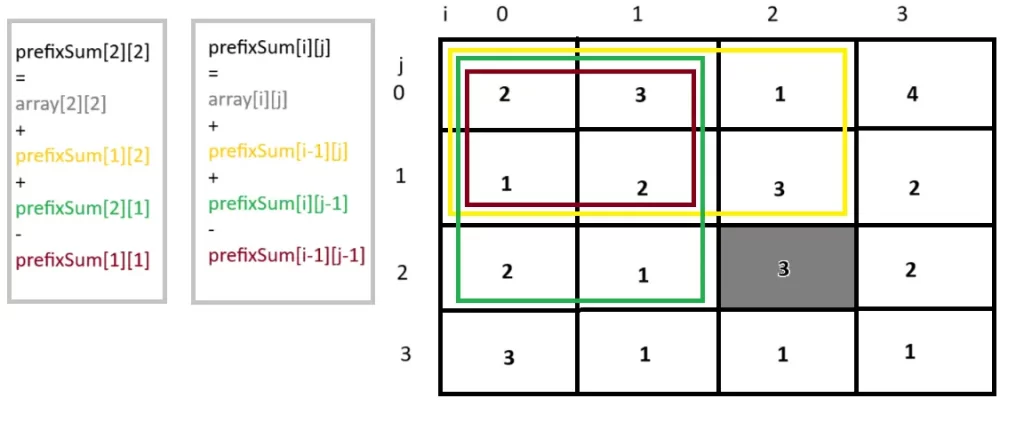
The prefix sum for a 2D matrix is an auxiliary matrix where each element at index (i, j) is the sum of all elements in the matrix from (0, 0) to (i, j).

Formula:-

prefix[i][j] = matrix[i][j]
              + prefix[i-1][j] (if i > 0)
              + prefix[i][j-1] (if j > 0)
              - prefix[i-1][j-1] (if i > 0 and j > 0)

Here, prefix[i-1][j-1] is subtracted because it is added twice in the prefix sums above and to the left.

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
        int[][] prefixSum = compute2DPrefixSum(matrix);
        System.out.println(Arrays.deepToString(prefixSum));
        // [[1, 3, 6], [5, 12, 21], [12, 27, 45]]
    }

    private static int[][] compute2DPrefixSum(int[][] matrix) {
        int rows = matrix.length, cols = matrix[0].length;
        int[][] prefixSum = new int[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                prefixSum[i][j] = matrix[i][j] 
                        + (i > 0 ? prefixSum[i - 1][j] : 0) 
                        + (j > 0 ? prefixSum[i][j - 1] : 0)
                        - (i > 0 && j > 0 ? prefixSum[i - 1][j - 1] : 0);
            }
        }
        return prefixSum;
    }
}

Range Sum Queries in 2D Matrices

To efficiently handle range sum queries in a 2D matrix, you can use the 2D prefix sum technique. This approach enables quick calculation of the sum of elements within any submatrix.

To find the sum of elements in a submatrix from (r1, c1) to (r2, c2) using a 2D prefix sum matrix, you can use the following formula:-

Sum = prefix[r2][c2]
      - prefix[r1-1][c2] (if r1 > 0)
      - prefix[r2][c1-1] (if c1 > 0)
      + prefix[r1-1][c1-1] (if r1 > 0 and c1 > 0)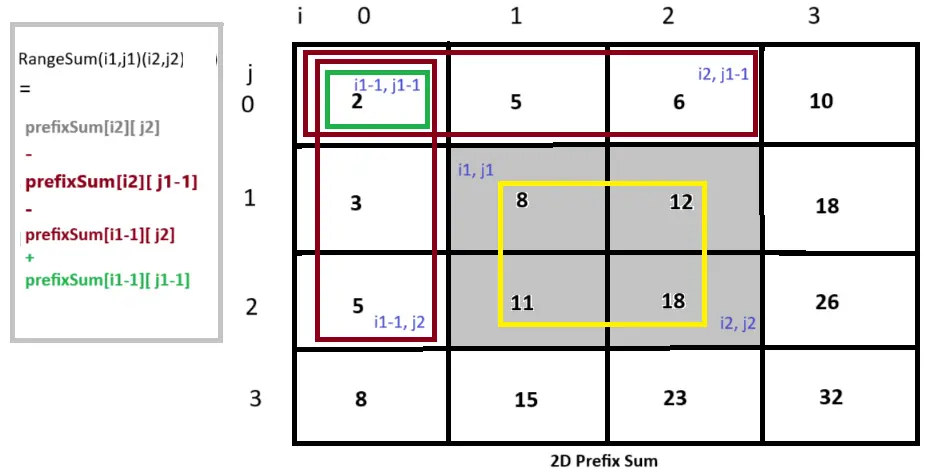

public class Test {
    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
        int[][] prefixSum = compute2DPrefixSum(matrix);
        System.out.println("Sum of submatrix (1, 1) to (2, 2): " 
               + rangeSumQuery(prefixSum, 1, 1, 2, 2)); // Output: 28
    }

    // Add compute2DPrefixSum() method

    private static int rangeSumQuery(int[][] prefixSum, int i1, int j1, int i2, int j2) {
        return prefixSum[i2][j2] 
                - (i1 > 0 ? prefixSum[i1 - 1][j2] : 0) 
                - (j1 > 0 ? prefixSum[i2][j1 - 1] : 0)
                + (i1 > 0 && j1 > 0 ? prefixSum[i1 - 1][j1 - 1] : 0);
    }
}

Range Update Queries on a 2D Array

Given a 2D array of integers, perform multiple update queries. Each query specifies a submatrix and an increment value. For each query, increase every element in the specified submatrix by the given value. After performing all queries, print the resultant 2D array.

Input: A 2D array of integers.

Multiple queries, each having five integers r1, c1, r2, c2, x.
r1, c1: Starting row and column of the submatrix.
r2, c2: Ending row and column of the submatrix.
𝑥: The value by which elements within the submatrix are to be incremented.

Example:-

[
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9]
]

Queries:-
(0, 0, 1, 1, 1)
(1, 1, 2, 2, 2)

Output:-

[
  [2, 3, 3],
  [5, 8, 6],
  [7, 10, 11]
]

Approach:-

• Initialize Difference Matrix: Create a difference matrix diff with extra rows and columns to handle boundary cases.
• Process Each Query:
  • Update the corners of the submatrix specified by the query.
  • Increment the top-left corner by x.
  • Decrement the cells below and to the right of the bottom-right corner.
  • Adjust the bottom-right corner to avoid double subtraction.
• Compute the Prefix Sum:
  • Convert the difference matrix back to the resultant matrix using prefix sums.
  • Update the original matrix with the computed values.
• Add prefix sum matrix and original matrix.

import java.util.Arrays;

public class Test {
    public static void main(String[] args) {
        int[][] matrix = {
            {2, 3, 2, 3, 5},
            {2, 3, 2, 3, 5},
            {2, 3, 2, 3, 5},
            {2, 3, 2, 3, 5},
            {2, 3, 2, 3, 5}
        };

        // top-left row, top-left col, bottom-right row, 
        // bottom-right col, increment value
        int[][] queries = {
            {0, 0, 2, 2, 1},
            {1, 1, 4, 4, 2},
            {3, 3, 3, 3, 3}
        };

        rangeUpdateQueries2D(matrix, queries);
        System.out.println(Arrays.deepToString(matrix));
    }

    private static void rangeUpdateQueries2D(int[][] matrix, int[][] queries) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        // Difference array with extra row and column
        int[][] diff = new int[rows + 1][cols + 1]; 

        // Step 1: Process each query and update the difference array
        for (int[] query : queries) {
            int r1 = query[0];
            int c1 = query[1];
            int r2 = query[2];
            int c2 = query[3];
            int x = query[4];

            diff[r1][c1] += x;
            if (r2 + 1 < rows) {
                diff[r2 + 1][c1] -= x;
            }
            if (c2 + 1 < cols) {
                diff[r1][c2 + 1] -= x;
            }
            if (r2 + 1 < rows && c2 + 1 < cols) {
                diff[r2 + 1][c2 + 1] += x;
            }
        }

        // Step 2: Compute the prefix sum for the difference array to get the final matrix
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (i > 0) {
                    diff[i][j] += diff[i - 1][j];
                }
                if (j > 0) {
                    diff[i][j] += diff[i][j - 1];
                }
                if (i > 0 && j > 0) {
                    diff[i][j] -= diff[i - 1][j - 1];
                }
                matrix[i][j] += diff[i][j];
            }
        }
    }
}

Output:-

[
  [3, 4, 3, 3, 5], 
  [3, 6, 5, 5, 7], 
  [3, 6, 5, 5, 7], 
  [2, 5, 4, 8, 7], 
  [2, 5, 4, 5, 7]
]

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!