Stack Data Structure - Know Program

Stack Data Structure | The Stack follows the FIFO (first in first out) order. The insertion is called PUSH, and the deletion is called POP. Elements are added and removed from the top. Stack Operations:-

isEmpty(): Returns true if stack is empty, else false.
push(x): Inserts an item to the top of the stack.
pop(): Removes an item from the top.
peek(): Returns the top item.
size(): Returns the size of stack.

Table of Contents

Stack Implementation in Java
Stack in Java
1. Check for Balanced Parenthesis in a String
Implement Two Stacks in an Array
2. Implement K Stacks in an Array
3. Stock Span Problem
4. Previous Greater Element
5. Next Greater Element
6. Largest Rectangular Area in a Histogram
7. Largest Rectangle with All 1’s
8. Stack with getMin() in O(1)
9. Infix, Prefix, and Postfix Conversion
- a. Infix to Postfix and Prefix Conversion
- b. Prefix to Infix Conversion
10. Evaluation of Postfix and Prefix Expressions
- a. Evaluation of Postfix Expression
- b. Evaluation of Prefix Expression

import java.util.Stack;

public class StackExample {
    public static void main(String[] args) {
        Stack<Integer> s = new Stack<>();

        // Push elements onto the stack
        s.push(15);
        s.push(20);
        s.push(35);

        // Peek the top element
        System.out.println(s.peek());

        // Pop the top element
        s.pop();
        System.out.println(s.peek());

        // Print the size of the stack
        System.out.println(s.size());

        // Push another element
        s.push(5);
        System.out.println(s.peek());

        // Check if the stack is empty
        System.out.println(s.isEmpty());
    }
}

Output:-

35
20
2
5
false

Corner conditions on Stack:-

Overflow: When push() called on a full stack. In Java, the Stack class grows dynamically.
Underflow: when pop() or peek() is called on empty stack. Java throws EmptyStackException.

Stack Implementation in Java

Array Based Implementation with handling underflow and overflow conditions:-

public class MyStack {
    private int arr[];
    private int cap;
    private int top;

    public MyStack(int size) {
        arr = new int[size];
        cap = size;
        top = -1;
    }

    public boolean isEmpty() {
        return top == -1;
    }

    public boolean isFull() {
        return top == cap - 1;
    }

    public int size() {
        return top + 1;
    }

    public void push(int x) {
        if (isFull()) {
            System.out.println("Stack overflow. Unable to push " + x);
        } else {
            top++;
            arr[top] = x;
        }
    }

    public int pop() {
        if (isEmpty()) {
            System.out.println("Stack underflow. Unable to pop.");
            return -1;
        }
        int res = arr[top];
        top--;
        return res;
    }

    public int peek() {
        if (isEmpty()) {
            System.out.println("Stack is empty. Unable to peek.");
            return -1;
        }
        return arr[top];
    }
}

public class Test {
    public static void main(String[] args) {
        MyStack myStack = new MyStack(5);
        myStack.push(10);
        myStack.push(20);
        System.out.println(myStack.pop()); // 20
        System.out.println(myStack.size()); // 1
    }
}

Time complexity of all operation in worst case: O(1)

ArrayList Based Implementation for Dynamic Resizing

import java.util.ArrayList;

public class MyStack<T> {
    private ArrayList<T> al;

    public MyStack() {
        al = new ArrayList<>();
    }

    public boolean isEmpty() {
        return al.isEmpty();
    }

    public int size() {
        return al.size();
    }

    public void push(T x) {
        al.add(x);
    }

    public T pop() {
        if (isEmpty()) {
            System.out.println("Stack underflow. Unable to pop.");
            return null;
        }
        T res = al.get(al.size() - 1);
        al.remove(al.size() - 1);
        return res;
    }

    public T peek() {
        if (isEmpty()) {
            System.out.println("Stack is empty. Unable to peek.");
            return null;
        }
        return al.get(al.size() - 1);
    }
}

public class Test {
    public static void main(String[] args) {
        MyStack<Integer> myStack = new MyStack<>();
        myStack.push(10);
        myStack.push(20);
        System.out.println(myStack.pop());
        System.out.println(myStack.size());
    }
}

Time complexity of all operation in average case: O(1)

LinkedList Based Implementation

When an ArrayList exceeds its capacity, it needs to resize, which involves creating a new array and copying all elements over, leading to potential performance hits during resizing.

If your primary operations are push and pop (which are at the beginning), and you want constant time performance with less concern for memory overhead, LinkedList is a better choice for Stack implementation. If you have a relatively stable size and want better cache performance with less frequent insertions and deletions, ArrayList might be the way to go.

class Node {
    int data;
    Node next;

    public Node(int data) {
        this.data = data;
    }
}

public class MyStack {
    private Node head;
    private int size;

    public MyStack() {
        head = null;
        size = 0;
    }

    public boolean isEmpty() {
        return head == null;
    }

    public int size() {
        return size;
    }

    public void push(int x) {
        Node temp = new Node(x);
        temp.next = head; // Link the new node to the current head
        head = temp; // Update the head to the new node
        size++;
    }

    public int pop() {
        if (head == null) {
            System.out.println("Stack underflow. Unable to pop.");
            return Integer.MAX_VALUE;
        }
        int res = head.data;
        head = head.next;
        size--;
        return res;
    }

    public int peek() {
        if (head == null) {
            System.out.println("Stack underflow. Unable to pop.");
            return Integer.MAX_VALUE;
        }
        return head.data;
    }
}

public class Test {
    public static void main(String[] args) {
        MyStack myStack = new MyStack();
        myStack.push(10);
        myStack.push(20);
        System.out.println(myStack.pop()); // 20
        System.out.println(myStack.size()); // 1
    }
}

Time complexity of all operations are O(1) in worst case.

Applications of Stack
Here’s a brief overview of some common stack applications:

Function Calls: Manages function call information using the call stack.
Balanced Parentheses: Checks if expressions have balanced brackets.
Reversing Items: Reverses elements in a collection.
Infix to Prefix/Postfix: Converts infix expressions to prefix/postfix.
Evaluation of Postfix/Prefix: Evaluates postfix/prefix expressions.
Stock Span Problem: Solves problems like finding stock spans. [Asked a lot in interviews].
Undo/Redo: Implements undo/redo functionality in applications.
Navigation: Manages back/forward navigation in browsers.

Stack in Java

Collection
— List (I)
— Vector
— Stack
— Queue (I)
— Deque
— ArrayDeque

In Java Collection Stack is supported using 2 classes:- Stack and ArrayDeque. Stack class is child of Vector class. ArrayDeque class implements Deque interface.

In Java, both Stack and ArrayDeque can be used to implement stack-like behavior, but there are some key differences that may influence your choice:

Stack Class:

Inheritance: Stack is a subclass of Vector, which means it inherits the synchronized methods of Vector. This makes Stack thread-safe by default.
Legacy Class: Stack is considered a legacy class. It has been part of Java since version 1.0, and newer collections are preferred for stack operations.
Performance: Due to its synchronization, Stack might have performance overhead in single-threaded contexts.

When to use Stack:

When you need thread-safe operations without additional effort.
When working with legacy code that already uses Stack.

ArrayDeque Class:

Interface: ArrayDeque implements the Deque interface, making it a versatile double-ended queue. It can be used as both a stack and a queue.
Performance: ArrayDeque is not thread-safe but offers better performance in single-threaded contexts. It avoids the overhead of synchronization.
Efficiency: It provides efficient implementations for stack operations (push, pop, peek), as it is designed for LIFO operations.

When to use ArrayDeque:

For non-thread-safe environments where performance is critical.
When you need a modern, efficient stack implementation.
When you require both stack and queue functionalities in your application.

// Using Stack
import java.util.Stack;

Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
System.out.println(stack.pop()); // 2
System.out.println(stack.peek()); // 1

// Using ArrayDeque
import java.util.ArrayDeque;
import java.util.Deque;

Deque<Integer> dequeStack = new ArrayDeque<>();
dequeStack.push(1);
dequeStack.push(2);
System.out.println(dequeStack.pop()); // 2
System.out.println(dequeStack.peek()); // 1

In most modern applications, ArrayDeque is preferred due to its efficiency and flexibility. However, choose Stack if you specifically need its thread-safe properties or if you’re working with legacy code. In single threaded environment ArrayDeque is more preferred.

Both implementation internally uses dynamic size array implementation (not LinkedList) therefore all operations have time complexity O(1).

1. Check for Balanced Parenthesis in a String

Given a string of parentheses ({, }, (, ), [, ]), we need to check if this string is balanced or not. Problem: 29

S = “{[()]}” Output: Yes
S = “{(})” Output: No
S = “{[]}” Output: No
S = “{[()()]}” Output: Yes

In the context of parentheses, “balanced” means that each opening parenthesis ((, {, [) has a corresponding closing parenthesis (), }, ]), and the pairs of parentheses are correctly nested. The bracket which was opened recently should be closed first.

import java.util.ArrayDeque;
import java.util.Deque;

public class Test {
    public static void main(String[] args) {
        String str = "{[()]}";
        System.out.println(isBalanced(str)); // true
    }

    private static boolean isBalanced(String str) {
        Deque<Character> deque = new ArrayDeque<>();
        for (int i = 0; i < str.length(); i++) {
            char ch = str.charAt(i);
            if (ch == '(' || ch == '{' || ch == '[') {
                deque.push(ch);
            } else {
                if (deque.isEmpty()) {
                    return false;
                } else if (!matching(deque.peek(), ch)) {
                    return false;
                } else {
                    deque.pop();
                }
            }
        }
        return deque.isEmpty();
    }

    public static boolean matching(char a, char b) {
        return ((a == '(' && b == ')') || 
                (a == '{' && b == '}') || 
                (a == '[' && b == ']'));
    }
}

We can also take help of HashMap to store the parenthesis as follows:-

private static boolean isBalanced(String str) {
    // Map for matching parentheses pairs
    Map<Character, Character> map = Map.of('(', ')', '[', ']', '{', '}');
    Deque<Character> deque = new ArrayDeque<>();

    for (int i = 0; i < str.length(); i++) { 
        char ch = str.charAt(i);
        
        // If it's an opening parenthesis, push to stack
        if (map.containsKey(ch)) {
            deque.push(ch);
        } else { // If it's a closing parenthesis
            // Check if stack is empty or doesn't match the top of the stack
            if (deque.isEmpty() || ch != map.get(deque.peek())) {
                return false;
            }
            // Pop the matching opening parenthesis from stack
            deque.pop();
        }
    }

    // Stack should be empty if all parentheses are balanced
    return deque.isEmpty();
}

Implement Two Stacks in an Array

We are given an array, we need to implement two stacks in it. Sample:-

class TwoStacks
{
    int arr[];

    void push1(int x) { . . . }
    void push2(int x) { . . . }

    int pop1() { . . . }
    int pop2() { . . . }

    int size1() { . . . }
    int size2() { . . . }

    int top1() { . . . }
    int top2() { . . . }
}

To implement two stacks within a single array, you can divide the array into two parts. One stack will start from the beginning of the array and grow towards the end, while the other stack will start from the end of the array and grow towards the beginning. This ensures that the two stacks don’t overlap unless the array is full.

public class TwoStacks {
    private int[] arr;
    private int size;
    private int top1, top2;

    public TwoStacks(int size) {
        this.size = size;
        arr = new int[size];
        top1 = -1;
        top2 = size;
    }

    public void push1(int x) {
        if (top1 < top2 - 1) {
            arr[++top1] = x;
        } else {
            System.out.println("Stack Overflow in stack 1");
        }
    }

    public void push2(int x) {
        if (top1 < top2 - 1) {
            arr[--top2] = x;
        } else {
            System.out.println("Stack Overflow in stack 2");
        }
    }

    public int pop1() {
        if (top1 >= 0) {
            int x = arr[top1--];
            return x;
        }
        System.out.println("Stack Underflow in stack 1");
        return Integer.MIN_VALUE;
    }

    public int pop2() {
        if (top2 < size) {
            int x = arr[top2++];
            return x;
        }
        System.out.println("Stack Underflow in stack 2");
        return Integer.MIN_VALUE;
    }

    public int size1() {
        return top1 + 1;
    }

    public int size2() {
        return size - top2;
    }

    public int top1() {
        if (top1 >= 0) {
            return arr[top1];
        }
        System.out.println("Stack 1 is empty");
        return Integer.MIN_VALUE;
    }

    public int top2() {
        if (top2 < size) {
            return arr[top2];
        }
        System.out.println("Stack 2 is empty");
        return Integer.MIN_VALUE;
    }
}

public class Test {
    public static void main(String[] args) {
        TwoStacks ts = new TwoStacks(10);

        // Operations on stack 1
        ts.push1(10);
        ts.push1(20);
        ts.push1(30);

        System.out.println(ts.pop1()); // 30
        System.out.println(ts.top1()); // 20
        System.out.println(ts.size1()); // 2

        // Operations on stack 2
        ts.push2(100);
        ts.push2(200);
        ts.push2(300);

        System.out.println(ts.pop2()); // 300
        System.out.println(ts.top2()); // 200
        System.out.println(ts.size2()); // 2
    }
}

2. Implement K Stacks in an Array

Given an array, how to implement K stacks in it. Sample:-

class KStacks {
    int arr[], cap;

    void push(int x, int sn) { ... }
    int pop(int sn) { ... }
    bool isEmpty(int sn) { ... }
    int size(int sn) { ... }
    int top(int sn) { ... }
}

Here sn represents stackNumber. We will pass the stackNumber everywhere in all the function and the value for sn will be from 0 to k-1.

To do this, we’ll need a more complex approach that keeps track of multiple stacks using a single array. We’ll also maintain auxiliary arrays to help manage the multiple stacks.

Single Array for All Stacks: Use one array to store elements of all stacks.
Top of Each Stack: Use an array to store the index of the top element of each stack.
Next Array: Use an array to store the next free index in the array or to link indices for stacks.
Free Index: Use an integer to store the beginning of the free list.

class KStacks {
    private int[] arr;    // Array of size 'cap' to store actual content to be stored in stacks
    private int[] top;    // Array of size 'k' to store indexes of top elements of stacks
    private int[] next;   // Array of size 'cap' to store next entry in all stacks
    private int n, k;     // n = size of array, k = number of stacks
    private int free;     // To store the beginning index of the free list

    // Constructor to initialize k stacks in an array of size n
    public KStacks(int k, int n) {
        this.k = k;
        this.n = n;
        arr = new int[n];
        top = new int[k];
        next = new int[n];
        for (int i = 0; i < k; i++) {
            top[i] = -1;
        }
        free = 0;
        for (int i = 0; i < n - 1; i++) {
            next[i] = i + 1;
        }
        next[n - 1] = -1;  // -1 indicates the end of the free list
    }

    // Check if there is space available
    public boolean isFull() {
        return free == -1;
    }

    // Push x to stack number sn
    public void push(int x, int sn) {
        if (isFull()) {
            System.out.println("Stack Overflow");
            return;
        }

        int i = free;  // Store index of free slot
        free = next[i];  // Update the index of free slot to index of the next slot in free list
        next[i] = top[sn];  // Update next of top and then top for stack number 'sn'
        top[sn] = i;
        arr[i] = x;  // Push the element
    }

    // Pop from stack number sn
    public int pop(int sn) {
        if (isEmpty(sn)) {
            System.out.println("Stack Underflow");
            return Integer.MIN_VALUE;
        }

        int i = top[sn];  // Find index of top item in stack number 'sn'
        top[sn] = next[i];  // Change top to store next of previous top
        next[i] = free;  // Attach the previous top to the beginning of the free list
        free = i;
        return arr[i];
    }

    // Check if stack number 'sn' is empty
    public boolean isEmpty(int sn) {
        return top[sn] == -1;
    }

    // Size of stack number 'sn'
    public int size(int sn) {
        int count = 0;
        int i = top[sn];
        while (i != -1) {
            count++;
            i = next[i];
        }
        return count;
    }

    // Top element of stack number 'sn'
    public int top(int sn) {
        if (isEmpty(sn)) {
            System.out.println("Stack is empty");
            return Integer.MIN_VALUE;
        }
        return arr[top[sn]];
    }
}

3. Stock Span Problem

Given a list of daily stock prices, the stock span for a day is the number of consecutive days leading up to that day, including the current day, for which the price of the stock was less than or equal to the price on that day. Example:-

Input: [100, 80, 60, 70, 60, 75, 85]
Output: [1, 1, 1, 2, 1, 4, 6]

Explanation:

On day 1, the price is 100. The span is 1 since there are no previous days.
On day 2, the price is 80. The span is 1 since the previous day (100) is higher.
On day 3, the price is 60. The span is 1 since the previous days (100, 80) are higher.
On day 4, the price is 70. The span is 2 since the price of the previous day (60) is less than or equal to the current day’s price.
On day 5, the price is 60. The span is 1.
On day 6, the price is 75. The span is 4 (days 3, 4, 5 all have prices less than or equal to 75).
On day 7, the price is 85. The span is 6 (days 2, 3, 4, 5, 6 all have prices less than or equal to 85).

Input: [30, 20, 25, 28, 27, 29];
Output: 1 1 2 3 1 5

Corner cases:- If array is sorted in ascending order then span will be 1 to n. If the array is sorted in descending order then the span for every day is 1. The span for 1st day is always 1.

Input: [10, 20, 30, 40];
Output: [1, 2, 3, 4]

Input: [40, 30, 20, 10];
Output: [1, 1, 1, 1]

Naive solution: Consider every element as first element and go to the left to check for the span.

public class Test {
    public static void main(String[] args) {
        int[] arr = { 100, 80, 60, 70, 60, 75, 85 };
        for (int i = 0; i < arr.length; i++) {
            int span = 1;
            for (int j = i - 1; j >= 0 && arr[j] <= arr[i]; j--) {
                span++;
            }
            System.out.print(span + " "); // 1 1 1 2 1 4 6 
        }
    }
}

Worst case (when array is sorted in ascending order) time complexity: O(n^2)

A stack can be used to solve the problem efficiently. Here’s a high-level description of the algorithm:

Create an empty stack and initialize an array to store spans.
Iterate through each price in the list.
While the stack is not empty and the current price is greater than or equal to the price corresponding to the index on top of the stack, pop the stack.
If the stack becomes empty, the span for the current price is the index + 1.
Otherwise, the span for the current price is the difference between the current index and the index on top of the stack.
Push the current index onto the stack.
Continue the process for all prices.

import java.util.ArrayDeque;
import java.util.Deque;

public class Test {
    public static void main(String[] args) {
        int[] arr = { 100, 80, 60, 70, 60, 75, 85 };
        printSpan(arr);
    }

    private static void printSpan(int[] arr) {
        Deque<Integer> s = new ArrayDeque<>();
        s.push(0);
        System.out.print(1 + " ");
        for (int i = 1; i < arr.length; i++) {
            while (!s.isEmpty() && arr[s.peek()] <= arr[i]) {
                s.pop();
            }
            int span = s.isEmpty() ? i + 1 : i - s.peek();
            System.out.print(span + " ");
            s.push(i);
        }
    }
}

Time Complexity: O(n), Auxiliary space: O(n).
Related Problem: 901, 739

4. Previous Greater Element

Given an array of distinct integers, find the closest (position-wise) greater element on the left of every element. If there is no greater element on the left, then print -1. Examples:

Input: arr[] = [15, 10, 18, 12, 4, 6, 2, 8]
Output: -1 15 -1 18 12 12 6 12

Input: arr[] = [8, 10, 12]
Output: -1 -1 -1

Input: arr[] = [12, 10, 8]
Output: -1 12 10

import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;

public class Test {
    public static void main(String[] args) {
        int[] arr = { 15, 10, 18, 12, 4, 6, 2, 8 };
        System.out.println(Arrays.toString(previousGreaterEle(arr)));
        // [-1, 15, -1, 18, 12, 12, 6, 12]
    }

    private static int[] previousGreaterEle(int[] arr) {
        int[] result = new int[arr.length];
        Deque<Integer> s = new ArrayDeque<>();
        for (int i = 0; i < arr.length; i++) {
            while (!s.isEmpty() && s.peek() <= arr[i]) {
                s.pop();
            }
            result[i] = s.isEmpty() ? -1 : s.peek();
            s.push(arr[i]);
        }
        return result;
    }
}

Time Complexity: O(n)

5. Next Greater Element

Given an array of integers, find the next greater element (position-wise closest and on the right side) for every array element. Problem Link1, Link2 Examples:

Input: arr[] = {5, 15, 10, 8, 6, 12, 9, 18}
Output: 15, 18, 12, 12, 12, 18, 18, -1

Input: arr[] = {10, 15, 20, 25}
Output: 15, 20, 25, -1

Input: arr[] = {25, 20, 15, 10}
Output: -1, -1, -1, -1

import java.util.Arrays;
import java.util.Stack;

public class Test {
    public static void main(String[] args) {
        int[] arr = { 5, 15, 10, 8, 6, 12, 9, 18 };
        System.out.println(Arrays.toString(nextGreaterEle(arr)));
        // [15, 18, 12, 12, 12, 18, 18, -1]
    }

    public static int[] nextGreaterEle(int[] arr) {
        int n = arr.length;
        int[] result = new int[n];
        Stack<Integer> stack = new Stack<>();

        for (int i = n - 1; i >= 0; i--) {
            while (!stack.empty() && stack.peek() <= arr[i]) {
                stack.pop();
            }
            result[i] = stack.empty() ? -1 : stack.peek();
            stack.push(arr[i]);
        }

        return result;
    }
}

Time Complexity: O(n)

6. Largest Rectangular Area in a Histogram

Given an array representing the heights of bars in a histogram, find the largest rectangular area that can be formed in the histogram. Example:

Input: heights = [2, 1, 5, 6, 2, 3]
Output: 10

In the given example, the largest rectangle has an area of 10. This area is formed by the bars with heights [5, 6]. Problem Link:- 84. Understanding the problem – better. Efficient Solution

Naive Solution O(n^2)

Consider every element as the smallest bar, go to its left, and find the rectangle; the same is true for the right side.

public class Test {
    public static void main(String[] args) {
        int[] arr = { 2, 1, 5, 6, 2, 3 };
        System.out.println(getMaxArea(arr)); // 10
    }

    private static int getMaxArea(int[] arr) {
        int res = 0, n = arr.length;
        for (int i = 0; i < n; i++) {
            int curr = arr[i];
            // left side
            for (int j = i - 1; j >= 0; j--) {
                if (arr[j] >= arr[i]) {
                    curr += arr[i];
                } else {
                    break;
                }
            }
            // right side
            for (int j = i + 1; j < n; j++) {
                if (arr[j] >= arr[i]) {
                    curr += arr[i];
                } else {
                    break;
                }
            }
            res = Math.max(res, curr);
        }
        return res;
    }
}

Better Solution O(n)

import java.util.*;

public class Main {
    public static void main(String[] args) {
        int[] arr = { 2, 1, 5, 6, 2, 3 };
        System.out.println(getMaxArea(arr)); // 10
    }

    private static int getMaxArea(int[] arr) {
        int n = arr.length;
        int[] left = new int[n]; // Previous smaller element index
        int[] right = new int[n]; // Next smaller element index
        Deque<Integer> stack = new ArrayDeque<>();

        // Fill left array
        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
                stack.pop();
            }
            left[i] = (stack.isEmpty()) ? -1 : stack.peek();
            stack.push(i);
        }

        stack.clear();

        // Fill right array
        for (int i = n - 1; i >= 0; i--) {
            while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
                stack.pop();
            }
            right[i] = (stack.isEmpty()) ? n : stack.peek();
            stack.push(i);
        }

        // Calculate max area
        int maxArea = 0;
        for (int i = 0; i < n; i++) {
            int width = right[i] - left[i] - 1;
            int area = arr[i] * width;
            maxArea = Math.max(maxArea, area);
        }

        return maxArea;
    }
}

We can indeed simplify the solution to just two loops! We can calculate the left and right bounds within the same pass through the array. Here’s how we can do it:

Initialize: res = 0
Find the Previous Smaller Element for every element.
Find the Next Smaller Element for every element.
Do the following for every element arr[i]:
— curr = arr[i]
— curr += (i – ps[i] -1) * arr[i]
— curr += (ns[i] – i – 1) * arr[i]
— res = max(res, curr)
Return res

Efficient Solution O(n)

import java.util.*;

public class Main {
    public static void main(String[] args) {
        int[] arr = { 2, 1, 5, 6, 2, 3 };
        System.out.println(getMaxArea(arr)); // 10
    }

    private static int getMaxArea(int[] arr) {
        int n = arr.length;
        int maxArea = 0;
        Deque<Integer> stack = new ArrayDeque<>();

        for (int i = 0; i <= n; i++) {
            int height = (i == n) ? 0 : arr[i];
            while (!stack.isEmpty() && height < arr[stack.peek()]) {
                int h = arr[stack.pop()];
                int width = stack.isEmpty() ? i : i - stack.peek() - 1;
                maxArea = Math.max(maxArea, h * width);
            }
            stack.push(i);
        }

        return maxArea;
    }
}

Both approaches we’ve discussed have the same time complexity, (O(n)), where (n) is the number of elements in the array.

Better Approach: This approach uses two passes over the array to compute the left and right arrays for the next and previous smaller elements. Each element is pushed and popped from the stack at most once, leading to an overall time complexity of (O(n)).
Efficient Approach: This approach combines the calculations into a single loop where each element is pushed and popped from the stack at most once. This also results in a time complexity of (O(n)).

So, both approaches have the same time complexity, but the optimized approach is simpler and more elegant since it avoids the need for additional arrays (left and right) and directly computes the maximum area in a single pass. This often results in lower constant factors and better practical performance.

7. Largest Rectangle with All 1’s

Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area. Prerequisite to solve this problem: Largest Rectangular Area in a Histogram. Problem: 221. Solution. However this problem can be solved better by using DP.

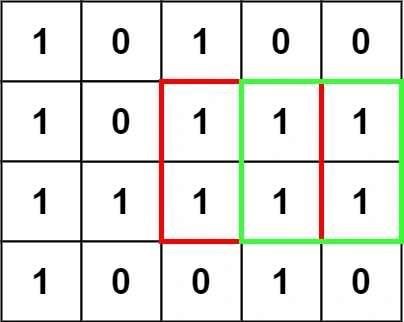
class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }

        int m = matrix.length;
        int n = matrix[0].length;
        int[] heights = new int[n];
        int maxSide = 0;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                heights[j] = (matrix[i][j] == '1') ? heights[j] + 1 : 0;
            }
            maxSide = Math.max(maxSide, maximalSquareInHistogram(heights));
        }

        return maxSide * maxSide;
    }

    private int maximalSquareInHistogram(int[] heights) {
        Deque<Integer> stack = new ArrayDeque<>();
        int maxSide = 0;
        int n = heights.length;

        for (int i = 0; i <= n; i++) {
            int height = (i == n) ? 0 : heights[i];
            while (!stack.isEmpty() && height < heights[stack.peek()]) {
                int h = heights[stack.pop()];
                int width = stack.isEmpty() ? i : i - stack.peek() - 1;
                int side = Math.min(h, width); // Ensure it's a square
                maxSide = Math.max(maxSide, side);
            }
            stack.push(i);
        }

        return maxSide;
    }
}

8. Stack with getMin() in O(1)

Let us first design a stack that supports getMin() in O(1).

Input: push(20), push(10), getMin(), push(5), getMin(), pop(), getMin(), pop(), getMin()
Output: 10 5 10 20

First Method: Assuming all elements are positive.

The idea is to use a variable for min.

import java.util.Stack;

public class MinStack {
    Stack<Integer> stack;
    int min;

    public MinStack() {
        stack = new Stack<>();
        min = Integer.MAX_VALUE;
    }

    void push(int x) {
        if (stack.isEmpty()) {
            min = x;
            stack.push(x);
        } else if (x <= min) {
            stack.push(x - min); // store negative value
            min = x;
        } else {
            stack.push(x);
        }
    }

    int getMin() {
        return min;
    }

    int peek() {
        int t = stack.peek();
        return t <= 0 ? min - t : t;
    }

    int pop() {
        int t = stack.pop();
        if (t <= 0) {
            int res = min;
            min = min - t; // Update min to the previous min
            return res;
        } else {
            return t;
        }
    }
}

public class Test {
    public static void main(String[] args) {
        MinStack minStack = new MinStack();
        minStack.push(5);
        minStack.push(10);
        minStack.push(20);
        System.out.println(minStack.getMin()); // 5

        minStack.push(2);
        System.out.println(minStack.getMin()); // 2

        minStack.push(6);
        minStack.push(4);
        System.out.println(minStack.getMin()); // 2
        minStack.pop();
        minStack.pop();

        minStack.push(2);
        minStack.pop();
        System.out.println(minStack.getMin()); // 2

        minStack.push(1);
        System.out.println(minStack.getMin()); // 1

        minStack.pop();
        minStack.pop();
        System.out.println(minStack.getMin()); // 5
    }
}

Time complexity for all operations (push(), pop(), peek(), getMin()) is O(1). However, this solution won’t work for the negative numbers. For that case, we can push 2*x – min into the stack. The previous solution extended as:-

public class MinStack {
    Stack<Integer> stack;
    int min;

    public MinStack() {
        stack = new Stack<>();
        min = Integer.MAX_VALUE;
    }

    void push(int x) {
        if (stack.isEmpty()) {
            min = x;
            stack.push(x);
        } else if (x <= min) {
            stack.push(2 * x - min); // Use 2 * x
            min = x;
        } else {
            stack.push(x);
        }
    }

    int getMin() {
        return min;
    }

    int peek() {
        int t = stack.peek();
        return t <= min ? min - t : t; // Use t <= min
    }

    int pop() {
        int t = stack.pop();
        if (t <= min) { // Use t <= min
            int res = min;
            min = 2 * min - t; // Use 2 * min
            return res;
        } else {
            return t;
        }
    }
}

How does this work? We push 2*x - min only when x <= min so 2*x - min is always going to be less than or equal to x, and x is going to be our new min.

9. Infix, Prefix, and Postfix Conversion

Infix: x+y
Postfix: xy+
Prefix: +xy

Advantages of Prefix and Postfix:-

Do not require parenthesis, precedence rules, and associativity rules.
Can be evaluated by writing a program that traverses the given expression exactly once.

Precedence and Associativity

In below table operators are given in lower precedence order:-

Operators	Associativity
^	Right to Left
*, /	Left to Right
+, –	Left to Right

Precedence: 10 + 20 * 2 => 10 + 40 => 50
Associativity (L to R): 10 + 2 – 3 => 12 – 3 => 9
Associativity (R to L): 2 ^ 1 ^ 2 = 2 ^ 1 = 2

Notation	Infix	Prefix	Postfix
Example 1	x + y * z	+ x * y z	x y z * +
Example 2	(x + y) * z	* + x y z	x y + z *

Steps for Infix to Postfix conversion:-

Expression = x + y * z
=> (x + (y * z))
=> (x + yz*) => xyz*+

Expression = (x + y) * z
=> ((x + y) * z)
=> (xy+ * z)
=> xy+z*

a. Infix to Postfix and Prefix Conversion

Infix Expression	Prefix Expression	Postfix Expression
a + b * c	+ a * b c	abc*+
(a + b) * c	* + a b c	ab+c*
a ^ b ^ c	^ a ^ b c	abc^^
(a + b) * (c + d)	* + a b + c d	ab+cd+*

Example of Infix to Postfix conversion

a + b * (c – d)
= (a + (b * (c – d))
= (a + (b * (cd-))
= (a + (bcd-*)
= abcd-*+
a + b * c / d + e
= (a + ((b * c) / d)) + e
= (a + (bc* / d)) + e
= (a + (bc*d/)) + e
= (abc*d/+) + e
= abc*d/+e+

In the table below operators are given in lower precedence order:-

Operators	Associativity
^	Right to Left
*, /	Left to Right
+, –	Left to Right

We will first add parenthesis to the expression, then convert the innermost expression to postfix, and then convert the outer expression to postfix.

Infix to Postfix Conversion Algorithm:-

Initialize: Create an empty stack, ST.
Iterate: For each character X from the input infix expression (processed left to right):

Operand: If X is an operand, add it to the output.
Left Parenthesis: If X is a left parenthesis, push it onto ST.
Right Parenthesis: If X is a right parenthesis:
- Pop from ST and add to the output until a left parenthesis is encountered.
- Discard the left parenthesis.
Operator: If X is an operator:
- If ST is empty, push X onto ST.
- Else, compare X with the operator on top of ST:
- Higher precedence: Push X onto ST.
- Lower or equal precedence:
  - Pop from ST and add to the output until an operator with lower precedence or a left parenthesis is encountered.
  - Push X onto ST.

Finalize: After processing all characters from the input infix expression, pop and add all remaining operators from ST to the output.

Note:-

Associativity: If two operators have the same precedence, associativity determines the order of evaluation (usually left-to-right for most operators).
Operator Precedence: Ensure proper handling of operator precedence to maintain the correct order of operations.

Infix to Postfix and Prefix Conversion

import java.util.Stack;

public class InfixConversion {
    // Method to return the precedence of an operator
    public static int precedence(char ch) {
        switch (ch) {
            case '+':
            case '-':
                return 1;
            case '*':
            case '/':
                return 2;
            case '^':
                return 3;
        }
        return -1;
    }

    // Method to convert infix to postfix
    public static String infixToPostfix(String exp) {
        StringBuilder result = new StringBuilder();
        Stack<Character> stack = new Stack<>();

        for (int i = 0; i < exp.length(); i++) {
            char c = exp.charAt(i);

            // If the character is an operand, add it to output
            if (Character.isLetterOrDigit(c)) {
                result.append(c);
            }
            // If the character is '(', push it to the stack
            else if (c == '(') {
                stack.push(c);
            }
            // If the character is ')', pop and output from the stack until '(' is found
            else if (c == ')') {
                while (!stack.isEmpty() && stack.peek() != '(') {
                    result.append(stack.pop());
                }
                stack.pop();
            } else { // An operator is encountered
                while (!stack.isEmpty() && precedence(c) <= precedence(stack.peek())) {
                    result.append(stack.pop());
                }
                stack.push(c);
            }
        }

        // Pop all the operators from the stack
        while (!stack.isEmpty()) {
            if (stack.peek() == '(') {
                return "Invalid Expression";
            }
            result.append(stack.pop());
        }

        return result.toString();
    }

    // Method to convert infix to prefix
    public static String infixToPrefix(String exp) {
        // Step 1: Reverse the infix expression
        exp = new StringBuilder(exp).reverse().toString();

        // Step 2: Replace '(' with ')' and vice versa
        exp = exp.replace('(', 'X');
        exp = exp.replace(')', '(');
        exp = exp.replace('X', ')');

        // Step 3: Get the postfix expression
        String postfix = infixToPostfix(exp);

        // Step 4: Reverse the postfix expression to get the prefix expression
        String prefix = new StringBuilder(postfix).reverse().toString();

        return prefix;
    }

    public static void main(String[] args) {
        String exp = "A*(B+C)/D";
        System.out.println("Infix: " + exp);
        System.out.println("Postfix: " + infixToPostfix(exp));
        System.out.println("Prefix: " + infixToPrefix(exp));
    }
}

b. Prefix to Infix Conversion

import java.util.Stack;

public class PrefixToInfix {
    // Check if the given character is an operator
    private static boolean isOperator(char c) {
        return c == '+' || c == '-' || c == '*' || c == '/' || c == '^';
    }

    // Convert prefix to infix expression
    public static String prefixToInfix(String prefix) {
        Stack<String> stack = new Stack<>();

        // Traverse the prefix expression from right to left
        for (int i = prefix.length() - 1; i >= 0; i--) {
            char c = prefix.charAt(i);

            // If the character is an operator
            if (isOperator(c)) {
                // Pop two operands from the stack
                String operand1 = stack.pop();
                String operand2 = stack.pop();

                // Combine the operands with the operator
                String infix = "(" + operand1 + c + operand2 + ")";

                // Push the resulting expression back to the stack
                stack.push(infix);
            } else {
                // If the character is an operand, push it to the stack
                stack.push(String.valueOf(c));
            }
        }

        // The final element of the stack will be the infix expression
        return stack.pop();
    }

    public static void main(String[] args) {
        String prefix = "*+AB-CD";
        System.out.println("Infix Expression: " + prefixToInfix(prefix));
    }
}

10. Evaluation of Postfix and Prefix Expressions

a. Evaluation of Postfix Expression

Initialize an empty stack.
Iterate through each character in the postfix expression.
For each character:

If it is an operand, push it onto the stack.
If it is an operator, pop the required number of operands from the stack, perform the operation, and push the result back onto the stack.

At the end, the stack will contain the result of the postfix expression.

import java.util.Stack;

public class PostfixEvaluation {
    // Method to evaluate postfix expression
    public static int evaluatePostfix(String exp) {
        // Create a stack
        Stack<Integer> stack = new Stack<>();

        // Scan all characters one by one
        for (int i = 0; i < exp.length(); i++) {
            char c = exp.charAt(i);

            // If the character is a digit, push it to the stack
            if (Character.isDigit(c)) {
                stack.push(c - '0');
            } 
            // If the character is an operator, pop two elements from the stack, 
            // apply the operator and push the result back
            else {
                int val1 = stack.pop();
                int val2 = stack.pop();

                switch (c) {
                    case '+':
                        stack.push(val2 + val1);
                        break;
                    case '-':
                        stack.push(val2 - val1);
                        break;
                    case '*':
                        stack.push(val2 * val1);
                        break;
                    case '/':
                        stack.push(val2 / val1);
                        break;
                }
            }
        }
        // The result is the only element left in the stack
        return stack.pop();
    }

    public static void main(String[] args) {
        String exp = "231*+9-";
        System.out.println("Postfix Expression: " + exp);
        System.out.println("Evaluation Result: " + evaluatePostfix(exp)); // -4
    }
}

b. Evaluation of Prefix Expression

Read the prefix expression from right to left.
Initialize an empty stack.
For each character in the expression:

If it is an operand, push it onto the stack.
If it is an operator, pop the required number of operands from the stack, apply the operator, and push the result back onto the stack.

At the end, the stack will contain the result of the prefix expression.

Java Program for Prefix Evaluation

import java.util.Stack;

public class PrefixEvaluation {
    // Method to evaluate prefix expression
    public static int evaluatePrefix(String exp) {
        Stack<Integer> stack = new Stack<>();

        // Scan the expression from right to left
        for (int i = exp.length() - 1; i >= 0; i--) {
            char c = exp.charAt(i);

            // If the character is an operand, push it to the stack
            if (Character.isDigit(c)) {
                stack.push(c - '0');
            } 
            // If the character is an operator, pop two elements from the stack, 
            // apply the operator and push the result back
            else {
                int val1 = stack.pop();
                int val2 = stack.pop();

                switch (c) {
                    case '+':
                        stack.push(val1 + val2);
                        break;
                    case '-':
                        stack.push(val1 - val2);
                        break;
                    case '*':
                        stack.push(val1 * val2);
                        break;
                    case '/':
                        stack.push(val1 / val2);
                        break;
                }
            }
        }
        // The result is the only element left in the stack
        return stack.pop();
    }

    public static void main(String[] args) {
        String exp = "-+*2319";
        System.out.println("Prefix Expression: " + exp);
        System.out.println("Evaluation Result: " + evaluatePrefix(exp));
    }
}

Example Walkthrough: Let’s walk through the evaluation of the prefix expression -+*2319:

Initial Expression: -+*2319
Reading from right to left:

Push 9 onto the stack: Stack = [9]
Push 1 onto the stack: Stack = [9, 1]
Push 3 onto the stack: Stack = [9, 1, 3]
Push 2 onto the stack: Stack = [9, 1, 3, 2]
Apply * to 2 and 3, push result 6: Stack = [9, 1, 6]
Apply + to 6 and 1, push result 7: Stack = [9, 7]
Apply - to 7 and 9, push result -2: Stack = [-2]

Final Result: The stack now contains the final result of the prefix expression: -2

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!