Menu Driven Program for Matrix Operations in Java

Menu Driven Program for Matrix Operations in Java | Program description:- Write a Java program for the menu-driven program for matrix operations. Perform matrix addition, subtraction, multiplication, and transpose using the switch case. Take the help of the methods.

Previously we had developed multiple Java programs on matrices like,

1. Program to Print 3×3 Matrix
2. Sum of matrix elements in Java 
3. Sum of diagonal elements in Java
4. Find out each row sum and column sum of a matrix
5. Addition of two Matrix in Java
6. Subtraction of two matrices in Java
7. Multiplication of two Matrix in Java
8. Transpose of a matrix in Java

Now, let us develop a program to perform various matrix operations addition, subtraction, multiplication, transpose using switch-case statement and method concept.

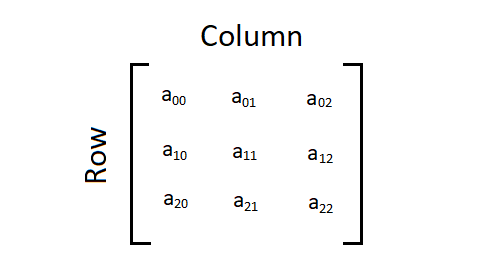
Matrix is a two-dimensional array. And to represent the two-dimensional array there should be two loops, where outer loops represent rows of the matrix and the inner loop represents the column of the matrix. See more:- Matrix in Java

Menu Driven Java Program for Matrix Operations (Addition, Subtraction, Multiplication, Transpose)

import java.util.Arrays;
import java.util.Scanner;

public class Matrix {

  // main method
  public static void main(String[] args) {

    // Scanner class object
    Scanner scan = new Scanner(System.in);

    // declare two matrix
    int a[][] = { { 5, 6, 7 }, { 8, 9, 10 }, { 3, 1, 2 } };
    int b[][] = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };

    // create third matrix
    int c[][] = new int[3][3];

    // display both matrix
    System.out.println("A = " + Arrays.deepToString(a));
    System.out.println("B = " + Arrays.deepToString(b));

    // variable to take choice
    int choice;

    // menu-driven
    do {
      // menu to choose the operation
      System.out.println("\nChoose the matrix operation,");
      System.out.println("----------------------------");
      System.out.println("1. Addition");
      System.out.println("2. Subtraction");
      System.out.println("3. Multiplication");
      System.out.println("4. Transpose");
      System.out.println("5. Exit");
      System.out.println("----------------------------");
      System.out.print("Enter your choice: ");
      choice = scan.nextInt();

      switch (choice) {
      case 1:
        c = add(a, b);
        System.out.println("Sum of matrix: ");
        System.out.println(Arrays.deepToString(c));
        break;
      case 2:
        c = subtract(a, b);
        System.out.println("Subtraction of matrix: ");
        System.out.println(Arrays.deepToString(c));
        break;
      case 3:
        c = multiply(a, b);
        System.out.println("Multiplication of matrix: ");
        System.out.println(Arrays.deepToString(c));
        break;
      case 4:
        System.out.println("Transpose of the first matrix: ");
        c = transpose(a);
        System.out.println(Arrays.deepToString(c));
        System.out.println("Transpose of the second matrix: ");
        c = transpose(b);
        System.out.println(Arrays.deepToString(c));
        break;
      case 5:
        System.out.println("Thank You.");
        return;
      default:
        System.out.println("Invalid input.");
        System.out.println("Please enter the correct input.");
      }
    } while (true);
  }

  // method to perform matrix addition and
  // return resultant matrix
  public static int[][] add(int[][] a, int[][] b) {

    // calculate row and column size of anyone matrix
    int row = a.length;
    int column = a[0].length;

    // declare a matrix to store resultant value
    int sum[][] = new int[row][column];

    // calculate sum of two matrices
    for (int i = 0; i < row; i++) {
      for (int j = 0; j < column; j++) {
        sum[i][j] = a[i][j] + b[i][j];
      }
    }

    // return resultant matrix
    return sum;
  }

  // method to perform matrix subtraction and
  // return resultant matrix
  public static int[][] subtract(int[][] a, int[][] b) {

    // calculate row and column size of anyone matrix
    int row = a.length;
    int column = a[0].length;

    // declare a matrix to store resultant value
    int sub[][] = new int[row][column];

    // calculate sum of two matrices
    for (int i = 0; i < row; i++) {
      for (int j = 0; j < column; j++) {
        sub[i][j] = a[i][j] - b[i][j];
      }
    }

    // return resultant matrix
    return sub;
  }

  // method to perform matrix multiplication and
  // return resultant matrix
  // passed matrices can be square or non-square matrix
  public static int[][] multiply(int[][] a, int[][] b) {

    // find row size of first matrix
    int row = a.length;
    // find column size of second matrix
    int column = b[0].length;

    // declare new matrix to store result
    int product[][] = new int[row][column];

    // find product of both matrices
    // outer loop up to row of A
    for (int i = 0; i < row; i++) {
      // inner-1 loop utp0 column of B
      for (int j = 0; j < column; j++) {
        // assign 0 to the current element
        product[i][j] = 0;

        // inner-2 loop up to A[0].length
        for (int k = 0; k < a[0].length; k++) {
          product[i][j] += a[i][k] * b[k][j];
        }
      }
    }
    return product;
  }

  // method to find transpose of a matrix
  public static int[][] transpose(int[][] a) {

    // calculate row and column size
    int row = a.length;
    int column = a[0].length;

    // declare a matrix to store resultant
    int temp[][] = new int[row][column];

    // calculate transpose of matrix
    // outer loop for row
    for (int i = 0; i < row; i++) {
      // inner loop for column
      for (int j = 0; j < column; j++) {
        // formula
        temp[i][j] = a[j][i];
      }
    }

    // return resultant matrix
    return temp;
  }

}

Output:-

A = [[5, 6, 7], [8, 9, 10], [3, 1, 2]]
B = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 1
Sum of matrix:
[[6, 8, 10], [12, 14, 16], [10, 9, 11]]

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 2
Subtraction of matrix:
[[4, 4, 4], [4, 4, 4], [-4, -7, -7]]

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 3
Multiplication of matrix:
[[78, 96, 114], [114, 141, 168], [21, 27, 33]]

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 4
Transpose of the first matrix:
[[5, 8, 3], [6, 9, 1], [7, 10, 2]]
Transpose of the second matrix:
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 6
Invalid input.
Please enter the correct input.

Choose the matrix operation,
—————————-
1. Addition
2. Subtraction
3. Multiplication
4. Transpose
5. Exit
—————————-
Enter your choice: 5
Thank You.

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!